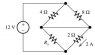
- #1
Orellanal
- 1
- 0
Homework Statement
Using Ohm's and Kirchoff's Rules find the unknown resistance Rx
Homework Equations
V = IR
Sum of currents at a node is zero
Sum of voltages around a loop is zero
The Attempt at a Solution
For the 2 ohm resistor I found the voltage to be 4V by the formula V = IR or V = 2A * 2ohm = 4 V
Therefore for the Rx resistor the voltage must also be 4 V as is it connected to the 2 ohm resistor in parallel.
The 4 and the 8 ohm resistors on top are connected in parallel and therefore must have the same voltage. 12 V - 8 V on the bottom two resistors gives 4 V for them which means that the voltage through each of the top resistors must be 2 V. Knowing this I then took Kirchoff's Current law at the nodes.
Node 2 (Right)
2V/ 8 ohm = 0.25 A (going into the node)
- 0.25 A + 2A = -1.75 A (going into the node)
Node 1 (Left)
-.5 A (into the node) + 1.75 A (going out of the node) = 1.25 A (going out of the node)
I then used ohm's law to find the resistance x by V = IR --> R = V/I or 4V/ 1.25 A = 3.2 ohms
which is wrong.
I thank you in advance for your help.