- #1
JohnnyIngrim
- 15
- 0
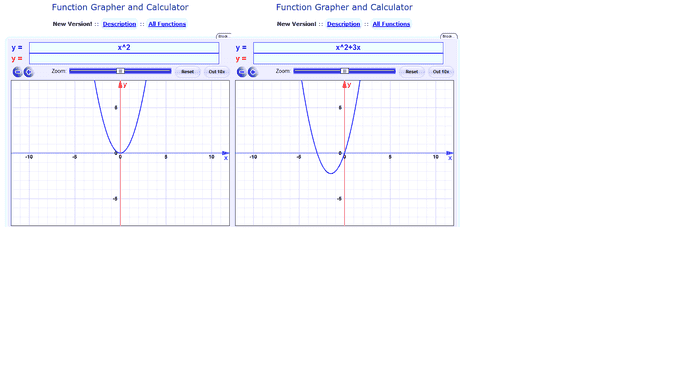
I get why it's a parabola because of the x^2 (for every value of x, y is the square of that number), but why does it shift to the left (and down as well) when I add x?