Question about mesh and node analysis

[Frank-95]

Hi, I'm trying to figure out if I haven't undestood the correct way to do a circuit analysis yet, or if I am just mistakening my calculi.

Here is a scheme of the circuit:

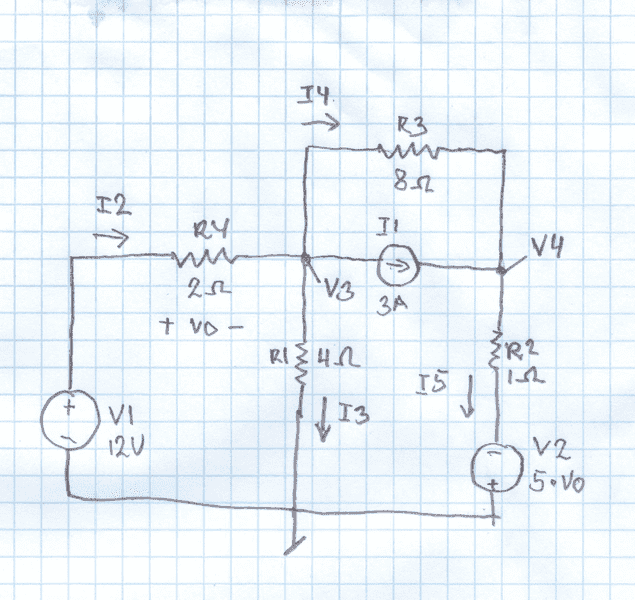
The component in the right bottom angle is a voltage dependent voltage source controlled by V0.

I tried to make a mesh anlysis at first, and I obtained the resulting system (considering the two mesh on the right as a supermesh):

-12 + 2i₁ + 4 (i₁ - i₂) = 0

-10i₁ - 4(i₁ - i₂) + 8i₃ + i₂ = 0

i₁ + i₂ = i₃ + 3

The results, for i₁, i₂ and i₃, are: 14/3, 4, 17/3

With this results V₀ would be 28/3, and the dependend source 140/3, which is wrong.

Can anyone help me to figure out the right process for such circuits? Thank you in advance

 

[Hesch]

What is the sign of V0 across R4 ?
( Attach +/- ).

 

[Frank-95]

It is a V₀, necessary to find the voltage source on the bottom right. The + is on the left the - on the right

 

[Hesch]

Well, I would make two nodes, V1 above R1 and V2 above R2.

Make two equations, using Kirchhoffs current law, to find V1 and V2. Afterwards you could find the currents usings ohms law, if desired.

( Pay attention to the signs ).

EDIT: Sorry, call the two nodes V3 and V4. ( V1 and V2 are used ).

 

[Frank-95]

In order to use the KVL I should consider nodes with source and resistance as a single supernode, right? It is what I thought at the beginning but I had (and still have) difficulties to immagine the incoming and outcoming current, and the supernode itself.

I mean, I can generally figure them out pretty easily, but I'm still getting used to this new argument of supernodes and supermesh

 

[Hesch]

You should not use KVL, because you don't know the voltage across a current source ( I1 ).

Attached a sketch with currents and nodes included. As for V3 you could write an equation:

I2 - I4 - I1 - I3 = 0 =>

( V1 - V3 ) / R4 - ( V3 - V4 ) / R3 - I1 - V3 / R1 = 0 ( you know V1, R4, R3, R1, I1 ).

Now write an equation as for V4 and find V3 and V4, then I4 = ( V3 - V4 ) / R3 , etc..

I've never heard of "supernodes".

 

[Jony130]

Because this circuit do not have any supernode.

 

[Frank-95]

That makes sense (and thanks for the image), but how can you know a priori which is the orientation of the current through R₁? It depends from both V₁ both V₂, but you don't know V₂ voltage, since it is dependent from V₀. For this I talked about supernodes and http://webcache.googleusercontent.com/search?q=cache:2ERIZA37kKYJ:www.electricaltechnology.org/2015/01/supermesh-circuit-analysis-step-step-solved-example.html+&cd=2&hl=it&ct=clnk&gl=it&client=ubuntu.

The use of the supermesh analysis let's you "skip" the current generator inside the mesh for KVL application, while the supernode analysis let's you "skip" the voltage generator for KCL. I tried both kinds of analysis: as regards the first one I don't know where I mistakened, as regards the second one I cannot figure out the two (one?) supernodes correctly and the incoming and outcoming currents.

EDIT: Jony130 a supernode isn't usually defined as a resistor and a voltage source in series during the application of the KCL?

 

[Hesch]

but how can you know a priori which is the orientation of the current through R1?

I cannot. I decide an orientation. Having decided a "wrong" orientation, the value of the current will just come out with a negative sign.

but you don't know V2 voltage, since it is dependent from V₀

V2 = 5 * V₀
V₀ = V1 - V3.

 

[Jony130]

: Jony130 a supernode isn't usually defined as a resistor and a voltage source in series during the application of the KCL?

Yes, you're right I missed that. But in this case we do not need to use a supernode because we know V2 value. V2 = 5*Vo = 5*(V1 - V3) and R2 current is V4 - V2. So we do not need a supernode here.

As for the mash

For I1 we have

-12V + I1*2Ω + 4Ω*(I1 - I2) = 0

for I3

I3 = -3A

and for I2 ??

 

[Frank-95]

Really thanks to both. Unluckily I don't have the right results so can you pease tell me if my steps are correct?

By nodes analysis I get (using this scheme):

i₂ = (v₁ - v₃) / 2
i₃ = v₃ / 4
i₄ = (v₃ - v₄) / 8
i₅ = v₄ - 5v₀ = v₄ - 5v₁ + 5v₃ (knowing that v₀ = v₁ - v₃)

i₂ = i₄ + 3 + i₃
i₁ + i₄ = i₅

v₁ / 2 - v₃ / 2 = v₃ / 8 - v₄ / 8 + i₁ + v₃ / 4
i₁ + v₃ / 8 - v₄/8 = v₄ - 5v₁ + 5v₃

Which results in this system:

7v₃ - v₄ = 24
39v₃ + 9v₄ = 504

Whose results are:

v₃ = 120/17 V = 7,06 V
v₄ = 432/17 V = 25,41 VBy mesh analysis I get (using this scheme)

5v₀ = 5(v₁ - v₃)
i₁ = (v₁ - v₃) / 2 -> v₃ = v₁ - 2i₁ -> 5v₀ = 10i₁

-12 + 2i₁ + 4(i₁ - i₂)
-10i₁ - 4(i₁ - i₂) + 8i₃ + i2 = 0

I have a doubt as regard the underlined voltage. Your scheme makes me suppose that the right formula is 8(i₃ + i₂), but actually my book says the contrary and considers only i₃

 

[Hesch]

As for node analysis, you get:

i5 = v4 - 5v0

It should be:

i₅ = v₄ - ( -5v₀ )

( Pay attention to the signs ).

Try again!

By means of ohms law, you can cross-check your results.

 

[Jony130]

As for the super node, we do not have any supper node because we "ground" V2 and V1 source. If for example we pick a ground at V3,then we will have two supernodes.

Really thanks to both. Unluckily I don't have the right results so can you pease tell me if my steps are correct?

By mesh analysis I get (using this scheme)

5v₀ = 5(v₁ - v₃)
i₁ = (v₁ - v₃) / 2 -> v₃ = v₁ - 2i₁ -> 5v₀ = 10i₁

-12 + 2i₁ + 4(i₁ - i₂)
-10i₁ - 4(i₁ - i₂) + 8i₃ + i2 = 0

I have a doubt as regard the underlined voltage. Your scheme makes me suppose that the right formula is 8(i₃ + i₂), but actually my book says the contrary and considers only i₃

EDIT

Why you have a minus sign here (- 4(i₁- i₂)) ?? And because this is a equation for loop 2 I2 current is the master, so the correct way is 4Ω * (I2 - I1)

And the correct way is 8(i₂ + i₃) again I2 is the master