Question about springs in series

  • Thread starter Thread starter Ovan
  • Start date Start date
  • Tags Tags
    Series Springs
AI Thread Summary
When two identical springs are placed in series and subjected to the same weight, the total compression is not simply the sum of the individual compressions. Each spring experiences the same force, leading to equal compression in both. The compression of each spring can be calculated using the formula ΔL=F/k, where F is the weight and k is the spring constant. Thus, if one spring compresses 5 inches under a 10-pound weight, both springs together will compress a total of 5 inches, not 10 inches. This understanding clarifies the mechanics of springs in series under a static load.
Ovan
Messages
3
Reaction score
0
Please help with this question, and if possible, please explain why.

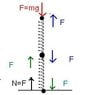
If one spring is compressed 5 inches by a 10 pound weight. How much is two identical springs in series compressed by the same weight (total compressed distance)?
 
Physics news on Phys.org
I'll try to ask you questions to lead you to the correct answer.

First, the way I understand the problem you have 4 objects, the weight, top spring, bottom spring, ground. Assuming that nothing is accelerating, what forces act on each object?
 
The force of the weight.

And am I correct to understand that this force acts equally on each spring?
Which would mean that both springs (in series) are compressed the same distance as the individual spring is. Which in return would mean that the springs in series would be compressed a total distance of 10 inches(twice as much as the single spring).

Is this correct?
 
If one spring with a certain compression C exerts force F, then what force would be produced by two springs, each with compression C?
 
Ovan said:
The force of the weight.

And am I correct to understand that this force acts equally on each spring?
Which would mean that both springs (in series) are compressed the same distance as the individual spring is. Which in return would mean that the springs in series would be compressed a total distance of 10 inches(twice as much as the single spring).

Is this correct?

It is basically correct.

The weight acts on the top spring. In equilibrium, there is no acceleration, so that force is balanced by the force of the top spring on the weight.For that, the spring has to be shortened by ΔL=F/k. (F is the external force, the weight of the object)

The tension is the same in the whole spring, so the top spring acts with force F at the top of the bottom spring. The bottom spring balances that force in equilibrium, so it exerts F force on the top spring. For that it has to be shortened by ΔL=F/k.

ehild
 

Attachments

  • serspr.JPG
    serspr.JPG
    7.6 KB · Views: 429
Thank you for your answer and explanation, much appreciated!
 

Thread '1:1 versus 2:1 Mechanical Advantage debate'

The rope is tied into the person (the load of 200 pounds) and the rope goes up from the person to a fixed pulley and back down to his hands. He hauls the rope to suspend himself in the air. What is the mechanical advantage of the system? The person will indeed only have to lift half of his body weight (roughly 100 pounds) because he now lessened the load by that same amount. This APPEARS to be a 2:1 because he can hold himself with half the force, but my question is: is that mechanical...
View full post »

Thread 'Average velocity as a weighted mean'

Hello everyone, Consider the problem in which a car is told to travel at 30 km/h for L kilometers and then at 60 km/h for another L kilometers. Next, you are asked to determine the average speed. My question is: although we know that the average speed in this case is the harmonic mean of the two speeds, is it also possible to state that the average speed over this 2L-kilometer stretch can be obtained as a weighted average of the two speeds? Best regards, DaTario
View full post »

Thread 'Newton's first law?'

Some physics textbook writer told me that Newton's first law applies only on bodies that feel no interactions at all. He said that if a body is on rest or moves in constant velocity, there is no external force acting on it. But I have heard another form of the law that says the net force acting on a body must be zero. This means there is interactions involved after all. So which one is correct?
View full post »

Similar threads

I Questions about a spring and its principle
Replies
9
Views
2K
I Work-Energy Theorem for Moving Block and Spring System?
Replies
4
Views
2K
Building a Marble Catapult
Replies
3
Views
875
Determining energy from spring arrangements (parallel&series)
Replies
2
Views
3K
Strength of springs - length of travel vs tension weight
Replies
1
Views
1K
How do dual-length springs with different tensions behave under external forces?
Replies
6
Views
7K
Does a Wheel with Movable Weights Require More Energy to Rotate?
Replies
26
Views
3K
B Why is my experimental spring constant an order of magnitude off?
Replies
4
Views
1K
I Understanding Bolted Joints: Shigley's Explanation & Real-Life Testing
Replies
8
Views
3K
Spring Constant and Spring Series
Replies
2
Views
2K

Hot Threads

Recent Insights

Back
Top