Question about the "Hat" tiling problem

[phyzguy]

TL;DR Summary

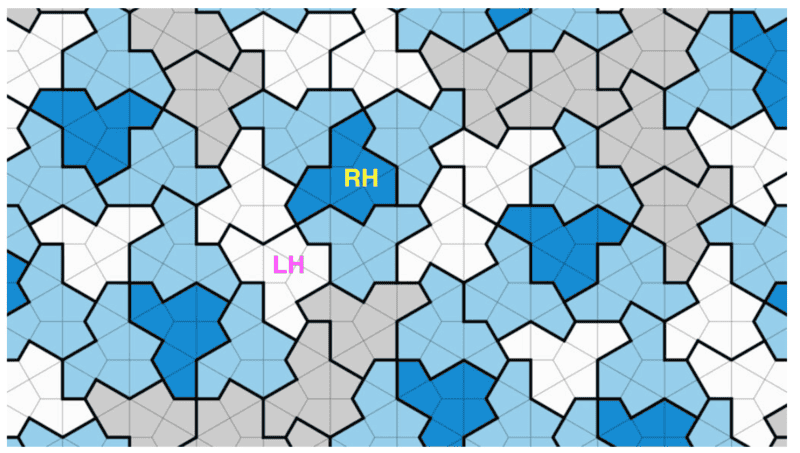
Is the "hat" shape really a single shape?

Recently there's been a lot of publicity about the discovery of a single shape that tiles the plane in a non-repeating manner. These are similar to Penrose tilings, but just use a single shape, while the Penrose tilings used two shapes. However, as I've played with these, I've realized that some of the "hats" are mirror images of others. So is it really fair to consider it a single shape? See the attached illustration showing that some shapes are right-handed(RH) and some are left-handed(LH). Is there a true single shape (without mirror imaging) that can do this? I'd appreciate comments.

 

[DaveC426913]

That's a good question.

Look up what kinds of transformations are allowed in tesselation. In particular, is flipping (rotation about a line) a permitted form of transformation? A quick Google search yields some ideas but not a definitive source as yet.

 

[pbuk]

So is it really fair to consider it a single shape?

I don't think "fairness" comes into it: what we have here is a single size of a single shape and its reflection which is clearly distinct from two distinct shapes without reflective symmetry such as the Penrose tiles (or multiple sizes of the same shape such as the Pinwheel tiles based on a concept by that other great modern polymath John Conway).

Is there a true single shape (without mirror imaging) that can do this?

The authors of the original paper address this in a follow-up paper https://arxiv.org/abs/2305.17743. The best resource to explore this is probably the website created by one of the authors Craig Caplan at https://cs.uwaterloo.ca/~csk/hat/.

 

[pbuk]

In particular, is flipping (rotation about a line) a permitted form of transformation?

Permitted by whom? There are no Transformation Police!

 

[DaveC426913]

Permitted by whom? There are no Transformation Police!

There are. Penrose tiling and other forms of aperiodic tiling do have their own rules.

(At the risk of letting the cat out of the bag) one of them is that flipping is a valid transformation. A flipped tile is the same tile, just as much as a translated or rotated tile is the same tile.

 

[pbuk]

There are. Penrose tiling and other forms of aperiodic tiling do have their own rules.

(At the risk of letting the cat out of the bag) one of them is that flipping is a valid transformation. A flipped tile is the same tile, just as much as a translated or rotated tile is the same tile.

No, this is not correct. It is true that there are classes of tilings that permit "flipping", however there are also classes that do not (and other classes where tiles are symmetrical so "flipping" is irrelevant), but there is no rule that says "noone may ever study tiling problems where flipping is not allowed".

This would be ridiculous and would mean that there would be no such thing as chiral monotiling as studied in the second paper I linked above.

 

[DaveC426913]

there is no rule that says "noone may ever study tiling problems where flipping is not allowed".

I did not suggest thus.

The way they are classified and distinguished is by their properties. If a given configuration doesn't meet the criteria, it is not part of the group being studied.

"Depending on the particular definitions of nonperiodicity and the specifications of what sets may qualify as tiles and what types of matching rules are permitted, the problem is either open or solved. "
- Wiki

My spurious examples:

• a solution to some hypothetical problem in aperiodic tilings can't have periodicity - periodicity is "not permitted" in the class that is being studied
• a solution to some hypothetical problem in regular tessellations can't use rhombuses - rhombuses are "not permitted" because a constraint on the group of regular tessellations is "made of regular polygons"

So the question to the OP is: what group of tilings does the hat solution fall into (what does it solve? what are the constraints on the problem?), and does that type of tiling include flipping?

 

[Tom.G]

So the question to the OP is: what group of tilings does the hat solution fall into (what does it solve? what are the constraints on the problem?), and does that type of tiling include flipping?

1) The tile covers the plane when flipping is allowed.
2) Iff the tile does not belong to an existing group,
Then a new group of 1 has been created.
QED

 

[pbuk]

Is there a true single shape (without mirror imaging) that can do this?

No. This was proven by Bhattacharya in 2016 and confirmed in a different proof by Terry Tao in 2020 referenced on his blog where he talks about work on this problem in higher dimensions.

 

[phyzguy]

No. This was proven by Bhattacharya in 2016 and confirmed in a different proof by Terry Tao in 2020 referenced on his blog where he talks about work on this problem in higher dimensions.

The article below says that the "specters" from the arXiv paper you linked in post #3, DO tile the plane aperiodically without reflections. That's also what I understood from reading that paper. So I'm confused by your post.

https://phys.org/news/2023-07-tiles-plane-aperiodically.html

 

[pbuk]

The article below says that the "specters" from the arXiv paper you linked in post #3, DO tile the plane aperiodically without reflections.

Yes, by my reading the claims about the Spectres do seem to be at odds with Bhattacharya's and Tao's proofs; however I am way out of my comfort zone here and cannot comment further.