- #1
lichen1983312
- 85
- 2
I have question about the proof of Cartan's structure equation in the context of pincipal bundle in Nakahara's book. The attached image is taken from the book.
To show that the curvature two-form ##\Omega ## satisfies
##\Omega (X,Y) = {d_P}\omega (X,Y) + [\omega (X),\omega (Y)]##
The author divided the proof into three cases: i, ##X,Y \in {H_u}P##, ii. ##X \in {H_u}P## and ##Y \in {V_u}P##, iii. ##X,Y \in {V_u}P##.
My problem is about the second case, the author said "Since ##Y \in {V_u}P##, there is an element ##V \in\mathfrak{g}
## such that ##Y = {V^\# }## (## V^\# ## being the fundamental vector field generated by ##V##) then ##\omega (Y) = V## is constant and hence ##X\omega (Y) = X \cdot V = 0##"
If I look at the context ##Y## is only required to be vertical such that ##{\left. Y \right|_u} \in {V_u}P##, so ##\omega (Y)## should depend on ##u \in P## such that ##{\omega _\mu }(Y) \ne {\omega _\nu }(Y)## in general. Am I right? Or the author is just trying to say that ##\omega (Y)## must be constant along ##X \in {H_u}P##? If this is the case then how to show it?
Thanks very much
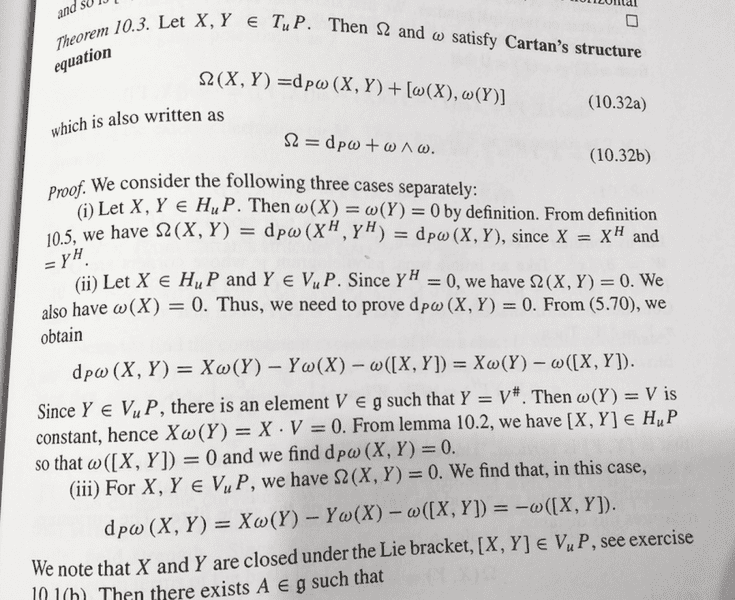
To show that the curvature two-form ##\Omega ## satisfies
##\Omega (X,Y) = {d_P}\omega (X,Y) + [\omega (X),\omega (Y)]##
The author divided the proof into three cases: i, ##X,Y \in {H_u}P##, ii. ##X \in {H_u}P## and ##Y \in {V_u}P##, iii. ##X,Y \in {V_u}P##.
My problem is about the second case, the author said "Since ##Y \in {V_u}P##, there is an element ##V \in\mathfrak{g}
## such that ##Y = {V^\# }## (## V^\# ## being the fundamental vector field generated by ##V##) then ##\omega (Y) = V## is constant and hence ##X\omega (Y) = X \cdot V = 0##"
If I look at the context ##Y## is only required to be vertical such that ##{\left. Y \right|_u} \in {V_u}P##, so ##\omega (Y)## should depend on ##u \in P## such that ##{\omega _\mu }(Y) \ne {\omega _\nu }(Y)## in general. Am I right? Or the author is just trying to say that ##\omega (Y)## must be constant along ##X \in {H_u}P##? If this is the case then how to show it?
Thanks very much
Last edited: