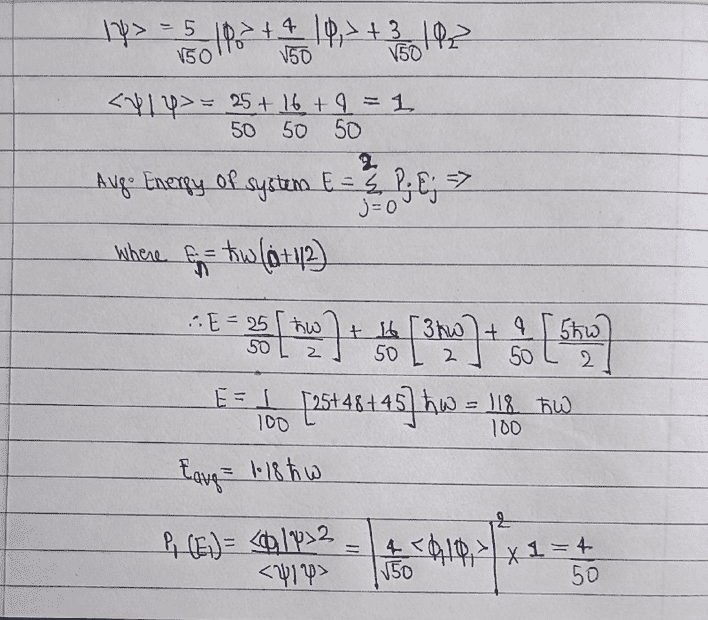Question on Intro QM pertaining to Harmonic Oscillator

[warhammer]

Homework Statement

Consider a system in a state
|ψ >=$frac{5/√50}*|φ0 > +frac{4/√50}*|φ1 > +frac{3/√50}*|φ2 >$
where |φ0 >, |φ1 > and |φ2 > are eigenstates of a harmonic oscillator
in ground, first and second excited state respectively.
(a) Find the average energy of this systemin the state |ψ >.
(b) What is the probability that |ψ > can be found in the state |φ1 >?

Relevant Equations

Avg Energy E=P(j)*E(j) (where E(n)=ℏw(n+0.5)
P(1)=$frac{|φ1|ψ>^2/<ψ|ψ >$

Hi. I have attached a neatly done solution to the above question. I request someone to please check my solution and help me rectify any possible mistakes that I may have made.

 

[kuruman]

Last line $4^2=16$. Other than that it looks good.

 

[warhammer]

Last line $4^2=16$. Other than that it looks good.

Ah yes! Sorry for that silly error, I noticed that now.

And thank you tons for your prompt guidance