- #1
- 1,126
- 643
- TL;DR Summary
- Difference between W(x) and Wn(x) ?
In the following I ask WA to solve the given equation and it produces a solution using the Lambert W function.
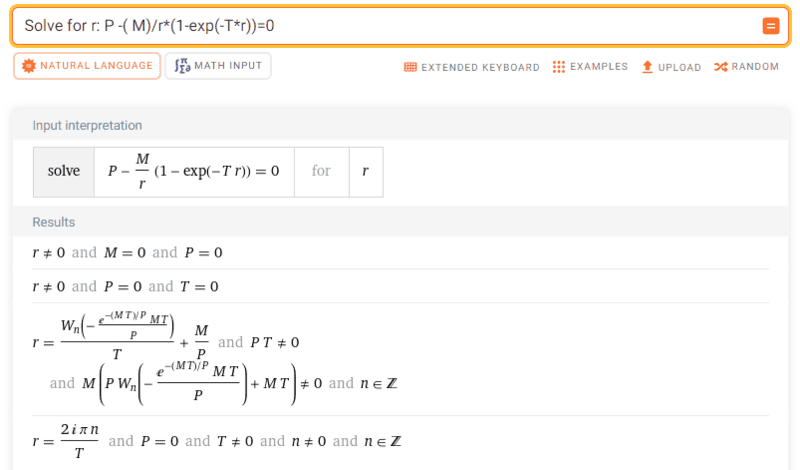
I thought : $$W(x*e^x) = x$$ but here it seems $$W_n \left(\frac{-MT}{P}*e^{\frac{-MT}{P}}\right) \neq \frac{-MT}{P}$$
Is there a difference between ##W(x)## and ##W_n(x)## ?
I thought : $$W(x*e^x) = x$$ but here it seems $$W_n \left(\frac{-MT}{P}*e^{\frac{-MT}{P}}\right) \neq \frac{-MT}{P}$$
Is there a difference between ##W(x)## and ##W_n(x)## ?
Last edited: