Dhmht_Kr
- 4
- 0
- Homework Statement
- Question is posted below.
- Relevant Equations
- completeness relation
Hi
Would you explain to me what is the q^ and how they are related to completeness.How can i solve this exercise?It is from "Quarks and leptons An Introductory course in Modern Particle Physics" of Halzen and Alan D.Martin.Also, can you point me to a useful bibliography?
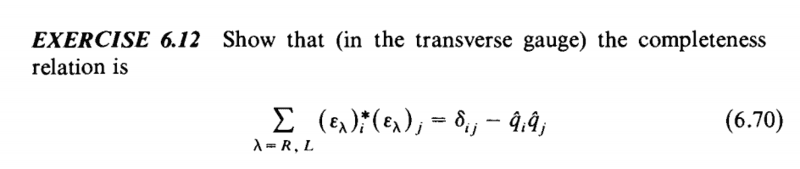
Would you explain to me what is the q^ and how they are related to completeness.How can i solve this exercise?It is from "Quarks and leptons An Introductory course in Modern Particle Physics" of Halzen and Alan D.Martin.Also, can you point me to a useful bibliography?