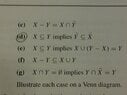- #1
shle
- 4
- 0
Hi, the question goes as follows:
Given two subsets X and Y of a universal set U, prove that: (refer to picture)
I'm having particular trouble on D and E, if anyone can clear this up or provide some clarification for me that would be appreciated! I know a venn diagram might not be possible here so just an explanation is ok
Thank you!
Given two subsets X and Y of a universal set U, prove that: (refer to picture)
I'm having particular trouble on D and E, if anyone can clear this up or provide some clarification for me that would be appreciated! I know a venn diagram might not be possible here so just an explanation is ok
Thank you!