Questions about these Trigonometry Graphs involving sin() and cos()

[pairofstrings]

TL;DR

a sin(x) - b cos(y) = y
a sin(x) + b cos(y) = 1

Hi.
I have two trigonometric equations whose graphs I am trying to understand.
Here are the equations:
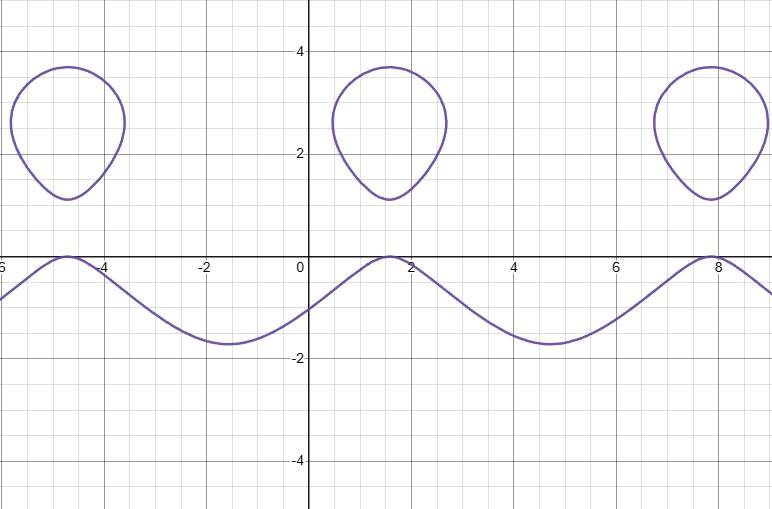
1. a sin(x) - b cos(y) = y; a = 2, b = 2

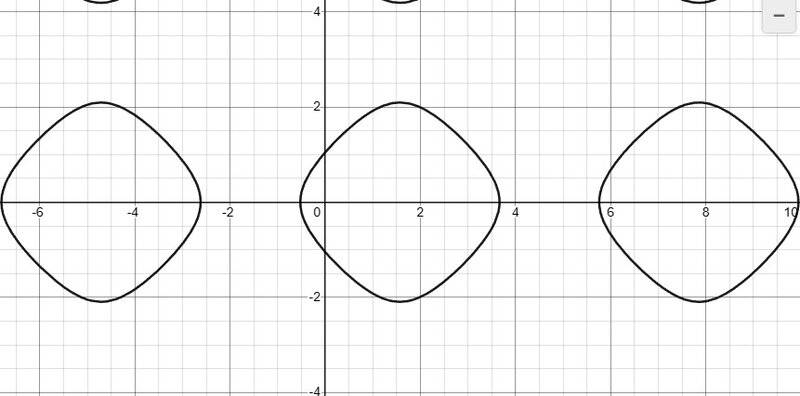
2. a sin(x) + b cos(y) = 1; a = 1, b = 1

My question is why the graphs are the way they are.
What should I do to understand them?
Can anyone explain these graphs?

Thanks for the help.

 

[wrobel]

When you consider level sets $\{(x,y)\mid f(x,y)=const\}$ it is important to find critical points of the function $f$ and understand which kind these critical points are.
So first find the points such that $df=0$.
It is like drawing a phase portrait of a Hamiltonian system with the Hamiltonian f.

 

[pairofstrings]

Thanks. So, I need to do Analysis first?

 

[PeroK]

Thanks. So, I need to do Analysis first?

The second graph looks off to me. You have
$$\cos y = 1 - \sin x$$If $\sin x <0$, then there are no solutions for $y$. You have solutions for $0 \le x \le \pi$, with symmetry about $x = \frac \pi 2$. Whatever solutions you have in this range are repeated every $2\pi$ units along the x-axis.

It would be better have units of $\pi$ along both axes.

Does that get you started?