Questions based on derivation of electrical potential energy

[gracy]

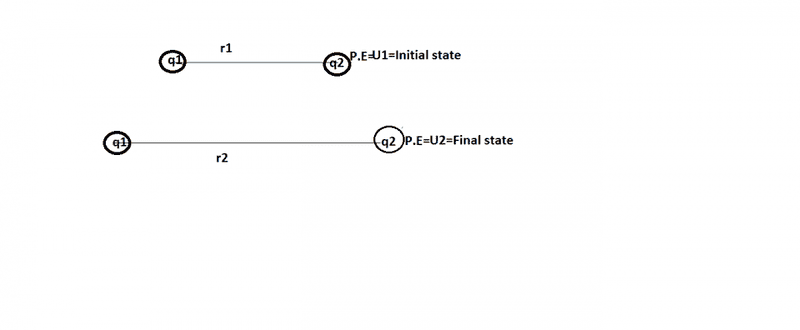
Consider a system of two charges $q_1$ and $q_2$ separated by distance $r_1$.This configuration is associated with a potential energy $U_1$.When the separation is increased to $r_2$.Potential energy becomes $U_2$

$dW_E$=$\vec{F}$.$\vec{dr}$

$dW_E$=$Fdrcos0$=$\frac{1}{4πε0}\frac{q_1q_2}{r^2}$dr

⇒$W_E$=$\int_{r_1}^{r_2}$$\frac{1}{4πε0}$$\frac{q_1q_2}{r^2}$dr

$W_E$=$\frac{-q_1q_2}{4πε0}$$[\frac{1}{r_2}$-$\frac{1}{r_1}]$

By definition of potential energy ,

$U_2$-$U_1$=$-W_E$

⇒$U_2$-$U_1$=$\frac{q_1q_2}{4πε0}$$[\frac{1}{r_2}$-$\frac{1}{r_1}]$

Taking infinity as reference i.e $r_1$=∞ and $U_1$=0

⇒$U_2$-0=$\frac{q_1q_2}{4πε0}$$[\frac{1}{r_2}$-$\frac{1}{∞}]$

⇒$U_2$=$\frac{1}{4πε0}$$\frac{q_1q_2}{r^2}$

Taking $U_2$=$U$ and $r_2$=$r_1$

$U$=$\frac{1}{4πε0}$$\frac{q_1q_2}{r}$

I want to ask as we can see $r_2$is >$r_1$

and then problem assumes $r_1$ to be ∞ my question is what is $r2$ then?how can $r_2$ be greater than $r_1$?How can any number be greater than infinity?

 

[jbriggs444]

The only place where I see an assumption that r2 > r1 is in the limits of integration in $W_E =\int_{r_1}^{r_2} \frac{1}{4πε0}\frac{q_1q_2}{r^2}dr$

But that is not an assumption that r2 > r1. You can evaluate an integral from a larger endpoint to a smaller. The result is the negative of the same integral evaluated from smaller to larger.

 

[Mister T]

I want to ask as we can see $r_2$is >$r_1$

This is what we see looking at the figure, yes.

and then problem assumes $r_1$ to be ∞

Yes, now they want you to imagine increasing $r_1$ so that it's not only bigger than $r_2$ but bigger than any value of $r$ you can imagine.

my question is what is $r2$ then?

They replaced $r_2$ with $r$, meaning that instead of thinking of it as a fixed value for the separation distance, it's now thought of as a variable.

how can $r_2$ be greater than $r_1$?

It can't. Very poorly authored example, if you ask me.

 

[gracy]

Yes, now they want you to imagine increasing $r_1$ so that it's not only bigger than $r_2$ but bigger than any value of $r$ you can imagine.

But they don't want to increase $r_1$ such that distance between them becomes greater than $r_2$ instead they want to increase $r_1$ such that distance between them becomes $r_2$

 

[haruspex]

But they don't want to increase $r_1$ such that distance between them becomes greater than $r_2$ instead they want to increase $r_1$ such that distance between them becomes $r_2$

Unless you have mistyped the final equation, it contains r, not r₁. So it's a misprint: they mean replacing r₂ with r.

 

[gracy]

So it's a misprint: they mean replacing r2 with r.

Yes.

 

[haruspex]

how can $r_2$ be greater than $r_1$?

It isn't. When you write an integral from a to b, there is no requirement for b to be greater than a:
$\int_a^bf(x)dx = -\int_b^af(x)dx$

 

[gracy]

When you write an integral from a to b, there is no requirement for b to be greater than a:

Yes,you have told me once.Upper and lower limit just indicate final and initial positions but this line confused me

When the separation is increased to $r_2$

 

[haruspex]

Yes,you have told me once.Upper and lower limit just indicate final and initial positions but this line confused me

Ok, but the equation is valid either way. With hindsight, the author might have preferred to write "changed to r₂".

 

[gracy]

I can also refer to this http://aakashtestguru.com/document/askExpert/08-10-2015-18:26:171608102015DP.pdf
for derivation of potential energy between the two charges ,right?

 

[Mister T]

But they don't want to increase $r_1$ such that distance between them becomes greater than $r_2$

Is this another typo then?

Taking infinity as reference i.e $r_1$=∞ and $U_1$=0

I suggest you present the entire example, as it was written by the author, along with a reference to the text you are quoting from.