- #1
Physics7
- 18
- 0
Questions -- solving pendulum period of rotation
Physical pendulum has a period of rotation
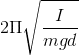
that changes by Changing the temperature.
According to the above show that the frequency shift of the pendulum would be:
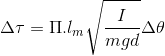
I have 2 questions,first solving the above question
and the second how Rotation period of the pendulum could be like this?
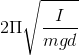
Physical pendulum has a period of rotation
that changes by Changing the temperature.
According to the above show that the frequency shift of the pendulum would be:
I have 2 questions,first solving the above question
and the second how Rotation period of the pendulum could be like this?
Last edited: