- #1
peasngravy
- 72
- 6
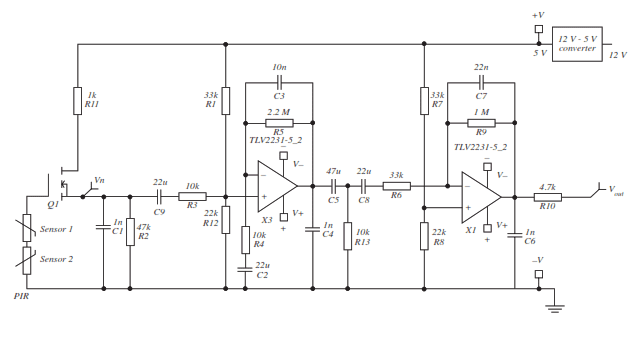
- Homework Statement
- Estimate the quiescent voltages at the inputs and outputs of the two
op-amps and the overall voltage gain (in decibels) of the circuit at the
frequency of operation. State any assumptions made.
- Relevant Equations
- None
Hi
I am completely stumped by this question - I have no idea where I am supposed to start with it. I have the answer to part a), which I had no trouble with.
Part B confuses me as I am not sure what the frequency of operation is. Would someone be able to help me to understand where to start with this?
Thanks
I am completely stumped by this question - I have no idea where I am supposed to start with it. I have the answer to part a), which I had no trouble with.
Part B confuses me as I am not sure what the frequency of operation is. Would someone be able to help me to understand where to start with this?
Thanks
