Rail Car with a Sail in the Wind

[MaratZakirov]

Homework Statement

The particle hits the sail which is installed on the rail car. Particle mass and velocity car mass is given in 2D. What would be particle and car velocities after collision?

Relevant Equations

$$ m_p\vec{v}_p^0 = m_p\vec{v}_p^1 + m_c\vec{v}_c $$
$$ \frac{1}{2}m_p\left \| \vec{v}_p^0 \right \|^2 = \frac{1}{2}m_p\left \| \vec{v}_p^1 \right \|^2 + \frac{1}{2}m_c\left \| \vec{v}_c \right \|^2 $$
$$ m_p<\vec{v}_p^0, \vec{n}> = m_p<\vec{v}_p^1, \vec{n}> $$

I solve the following problem, there is a particle of mass $m_p$ and velocity $\vec{v}_p$ which collide with sail installed on rail car with mass $m_c$ resting in the frame of reference associated with it before the collision. The cart is fixed on straight rails for which the vector $\vec{n}$ is normal. All velocities are given for the inertial frame of reference associated with the cart before colliding with a particle

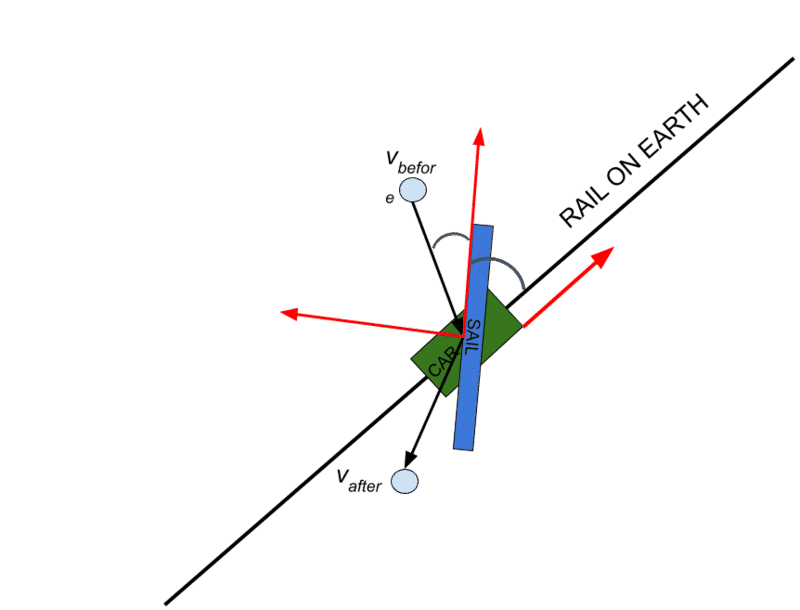
I wrote down three equations, two general ones and the last equation taking into account the orientation of the rails

First equation for moment conservation, which is always the case
$m_p\vec{v}_p^0 = m_p\vec{v}_p^1 + m_c\vec{v}_c$
Next energy conservation
$\frac{1}{2}m_p\left \| \vec{v}_p^0 \right \|^2 = \frac{1}{2}m_p\left \| \vec{v}_p^1 \right \|^2 + \frac{1}{2}m_c\left \| \vec{v}_c \right \|^2$
And third one is equation which say that in the normal to rail direction moment of particle is conserved after collision
$m_p<\vec{v}_p^0, \vec{n}> = m_p<\vec{v}_p^1, \vec{n}>$What is the difficulty ?

The point is that I do not understand how to write the equation taking into account the orientation of the sail, although it is obvious that the orientation of the sail is determining for this task, just like the orientation of the rails, but for the rails I seem to have written the equation, but for the sail I don’t know how.

 

[haruspex]

First equation for moment conservation, which is always the case

Momentum will not be conserved in the direction normal to the rails.

And third one is equation which say that in the normal to rail direction moment of particle is conserved after collision

Why?

 

[MaratZakirov]

Momentum will not be conserved in the direction normal to the rails.

Why?

My thoughts were the following:

I took momentum conservation equation:
$m_p\vec{v}_p^0 = m_p\vec{v}_p^1 + m_c\vec{v}_c$
then I made a scalar product for both sides of it
$<m_p\vec{v}_p^0, \vec{n}> = <m_p\vec{v}_p^1 + m_c\vec{v}_c, \vec{n}>$
simplified it a bit
$m_p<\vec{v}_p^0, \vec{n}> = m_p<\vec{v}_p^1, \vec{n}> + m_c<\vec{v}_c, \vec{n}>$
and then I realized that $<\vec{v}_c, \vec{n}>$ must be equal to zero because car can't have any velocity in the direction of $\vec{n}$
So finally I get my third equation
$m_p<\vec{v}_p^0, \vec{n}> = m_p<\vec{v}_p^1, \vec{n}>$

It seems "not OK" for me also because it turns out that the particle did not collide with the car at all. But I can't figure out what is wrong with these calculations above. And if you have ready to show equations for this task, I will be very grateful for that.

 

[haruspex]

My thoughts were the following:

I took momentum conservation equation:
$m_p\vec{v}_p^0 = m_p\vec{v}_p^1 + m_c\vec{v}_c$

As I posted, that is not applicable. There is a reaction impulse from the rail.
Only the component of momentum parallel to the rail will be conserved.

 

[MaratZakirov]

As I posted, that is not applicable. There is a reaction impulse from the rail.
Only the component of momentum parallel to the rail will be conserved.

What is "reaction impulse"?
Could you please kindly write some equations? Or maybe you provide links to some motivational examples similar to my case?

 

[Delta2]

What is "reaction impulse"

The impulse of the normal force from the rail . According to one model, this impulse completely neutralizes any possible component of velocity normal to the rail, after the collision.

That is the normal component of velocity after collision is zero for all the bodies of interest.

 

[MaratZakirov]

The impulse of the normal force from the rail . According to one model, this impulse completely neutralizes any possible component of velocity normal to the rail, after the collision.

That is the normal component of velocity after collision is zero for all the bodies of interest.

Any possible normal to the rail component of velocity of that object? Or both? How momentum conservation equation look in this case?

 

[Delta2]

Any possible normal to the rail component of velocity of that object? Or both? How momentum conservation equation look in this case?

the normal component of velocities of the car and the particle will be zero after the collision. The momentum conservation equation holds only for the parallel components before and after. That is $$m_p\vec{v}_{p\parallel}^0+m_c\vec{v}_{c\parallel}^0=m_p\vec{v}_{p\parallel}^1+m_c\vec{v}_{c\parallel}^1$$ to find the parallel components before the collision you need to know some angles.

 

[Delta2]

If you have done some conservation of momentum problems where we have conservation of momentum on the x-axis but not on the y-axis, its a very similar thing here.

 

[MaratZakirov]

the normal component of velocities of the car and the particle will be zero after the collision. The momentum conservation equation holds only for the parallel components before and after. That is $$m_p\vec{v}_{p\parallel}^0+m_c\vec{v}_{c\parallel}^0=m_p\vec{v}_{p\parallel}^1+m_c\vec{v}_{c\parallel}^1$$ to find the parallel components before the collision you need to know some angles.

First I must say that in equation you wrote $\vec{v}_{c\parallel}^0 = \vec{0}$ because the frame of reference is linked to the car before the collision and car do not have any velocity whatsoever before collision.

Angles are set by unit direction vectors $\vec{n}$ is normal to rail $\vec{r}$ is rail vector and $\vec{s}$ is vector normal to the sail.

You claim that perpendicular component of particle will be completely vanished after collision. From which law of physics does this follow? For example, a particle hitting a wall changes the sign of its perpendicular component without eliminating it in any way.

(Also, I prefer to work with scalar product instead of thinking about angles or parallel and perpendicular components of vectors. I believe these approaches are completely equivalent, but scalar products are more explicit and simpler.)

 

[Delta2]

First I must say that in equation you wrote v→c∥0=0→ because the frame of reference is linked to the car before the collision and car do not have any velocity whatsoever before collision.

Wait, do you mean that we are working in the accelerating frame of reference of the car (which is being accelerated collision after collision) or do you mean that initially the car's velocity is zero. This might be true for the first collision but for the second collision the car will have some velocity (unless you are working in the frame of reference of the car).

 

[Delta2]

You claim that perpendicular component of particle will be completely vanished after collision. From which law of physics does this follow? For example, a particle hitting a wall changes the sign of its perpendicular component without eliminating it in any way.

It follows from the momentum-impulse theorem, according to one model as I said. According to that model and to that theorem, the initial normal momentum minus the impulse from the normal force equals to zero(=the final momentum). According to another model it might cause vibrations of the car along the direction of normal.

That example you mention is only when the collision of the particle to wall is perfectly elastic. If it is perfectly inelastic the particle will lose all its velocity.

 

[MaratZakirov]

Wait, do you mean that we are working in the accelerating frame of reference of the car (which is being accelerated collision after collision) or do you mean that initially the car's velocity is zero. This might be true for the first collision but for the second collision the car will have some velocity (unless you are working in the frame of reference of the car).

Let's concentrate on the first collision.

Later on, we can always select a new frame of reference linked to a car before the next collision, for computer simulation purposes (if you're asking about that) it's not a problem at all to make such transformations just substitute car velocity when collision detecting system finds particle which is going to collide with car.

 

[Delta2]

well for the first collision according to my opinion it is $$\vec{v_{p\perp}}^1=\vec{v_{c\perp}}^1=0$$ and the other equation is the momentum equation for the parallel components as i wrote it in post #8 except that $\vec{v_{c\parallel}}^0=0$.

 

[MaratZakirov]

well for the first collision according to my opinion it is $$\vec{v_{p\normal}}^1=\vec{v_{c\normal}}^1=0$$ and the other equation is the momentum equation for the parallel components as i wrote it in post #8 except that $\vec{v_{c\parallel}}^0=0$.

What is the physical reason to $\vec{v}_{p\perp}^1=\vec{0}$ be true? In similar case particle and wall it is not true.

 

[Delta2]

What is the physical reason to v→p⊥1=0→ be true?

Well all right I agree after all that it might not be zero. But I think we need to know the normal force from the rail in order to determine it, using the momentum-impulse theorem.. Conservation of momentum simply doesn't hold in the normal direction because there is an external force acting, the normal force from the rail so what you did at post #3 is not correct because the starting equation is not valid.

 

[haruspex]

Let's concentrate on the first collision.

Later on, we can always select a new frame of reference linked to a car before the next collision, for computer simulation purposes (if you're asking about that) it's not a problem at all to make such transformations just substitute car velocity when collision detecting system finds particle which is going to collide with car.

You may be missing the point. In each collision the car is accelerated. This makes it very tricky to work in the frame of the car in regards to how quantities change from before to after the collision. Stick to the ground frame.

In each collision, if the car were on a frictionless surface, instead of rails, it would be accelerated in the $\hat n$ direction. The rails prevent that by exerting an impulse in the $\hat n$ direction. So the momentum of the particle + car system is not conserved in that direction.
Since the rail exerts no impulse normal to the $\hat n$ direction, i.e. parallel to the rails, the momentum of the particle + car system is conserved in that direction. Write the equation for that.

 

[MaratZakirov]

I finally have the solution (whether it is correct or not, I expect you to judge)

Given:

$\vec{v}_p$ and $m_p$ initial velocity and mass of particle.

$m_c$ is the mass of car which is on rail with unit vector $\vec{r}$ direction and unit (with length equal to 1) vector $\vec{s}$ as sail perpendicular vector

Task: is to find $\vec{v}_p^1$ and $\vec{v}_c$ (because initial is zero). Frame of reference is stick to car for simplicity.

1. Momentum conservation equation particle velocity divided into 2 parts parallel to $\vec{s}$ and perpendicular.

$m_p(\vec{v}_{p\parallel s} + \vec{v}_{p \perp s}) = m_p(\vec{v}_{p\parallel s} + \vec{v}_{p \perp s}) + m_c\vec{v}_c$

2. I claim that perpendicular to $\vec{s}$ part of particle velocity will remain the same after collision

$\vec{v}_{p\perp s} = \vec{v}_{p\perp s}^1$

3. Considering (2)

$m_p\vec{v}_{p\parallel s} = m_p\vec{v}_{p\parallel s}^1 + m_c\vec{v}_c$

4. Energy conservation equation (collision is rigid)

$\frac{1}{2}m_p\left | \vec{v}_p \right |^2 = \frac{1}{2}m_p\left | \vec{v}_p^1 \right |^2 + \frac{1}{2}m_c\left | \vec{v}_c \right |^2$

5. Trtansform (4)

$m_p\left | \vec{v}_p \right |^2 - m_p\left | \vec{v}_p^1 \right |^2 = m_c\left | \vec{v}_c \right |^2$

$m_p(\vec{v}_p - \vec{v}_p^1)(\vec{v}_p + \vec{v}_p^1) = m_c\left | \vec{v}_c \right |^2$

6. Membering (2) perpendicular part of particle velocity after the collision is the same

$m_p(\vec{v}_{p \parallel s} - \vec{v}_{p \parallel s}^1)(\vec{v}_{p \parallel s} + \vec{v}_{p \parallel s}^1 + 2\vec{v}_{p \perp s}) = m_c\vec{v}_c\vec{v}_c$

7. Considering (3)

$m_p(\vec{v}_{p\parallel s} - \vec{v}_{p\parallel s}^1) = m_c\vec{v}_c$

$\vec{v}_{p \parallel s} + \vec{v}_{p \parallel s}^1 + 2\vec{v}_{p \perp s} = \vec{v}_c$

8. I claim that parallel to $\vec{s}$ component of particle velocity perpendicular to $\vec{r}$ is remain the same after collision

$\vec{v}_{p \parallel s \perp r}^1 = \vec{v}_{p \parallel s \perp r}$

Proof:

Consider momentum conservation equation:

$m_p\vec{v}_{p \parallel s} = m_p\vec{v}_{p \parallel s}^1 + m_c\vec{v}_c$

then consider it in two parts: perpendicular to $\vec{r}$

$m_p\vec{v}_{p \parallel s \perp r} = m_p\vec{v}_{p \parallel s \perp r}^1 + m_c\vec{v}_{c \perp r}$

but $\vec{v}_c$ can not have any perpendicular to $\vec{r}$ component thus proof is ended

$m_p\vec{v}_{p \parallel s \perp r} = m_p\vec{v}_{p \parallel s \perp r}^1 + m_c\vec{0}$

9. Consider parllel to $\vec{r}$ particle

$m_p\vec{v}_{p \parallel s \parallel r} = m_p\vec{v}_{p \parallel s \parallel r}^1 + m_c\vec{v}_{c \parallel r}$

substitute $\vec{v}_c$ from (7) ($\vec{v}_{c \parallel r}=\vec{v}_{p \parallel s \parallel r} + \vec{v}_{p \parallel s \parallel r}^1 + 2\vec{v}_{p \perp s \parallel r}$)

then

$m_p\vec{v}_{p \parallel s \parallel r} = m_p\vec{v}_{p \parallel s \parallel r}^1 + m_c(\vec{v}_{p \parallel s \parallel r} + \vec{v}_{p \parallel s \parallel r}^1 + 2\vec{v}_{p \perp s \parallel r})$

10. Finally we got answer for $\vec{v}_{p \parallel s \parallel r}$

$\vec{v}_{p \parallel s \parallel r}^1 = \frac{m_p-m_c}{m_p + m_c}\vec{v}_{p \parallel s \parallel r} - \frac{2m_c}{m_p + m_c}\vec{v}_{p \perp s \parallel r}$

11. Using same logic we can get $\vec{v}_{c \parallel r} = \vec{v}_c$

$\vec{v}_c = \vec{v}_{c \parallel r} = \frac{2m_p}{m_p + m_c}(\vec{v}_{p \parallel s \parallel r} + \vec{v}_{p \perp s \parallel r})$

PS

What is for example $\vec{v}_{p \parallel s \perp r}$

$\vec{v}_{p \parallel s \perp r}=\frac{<\vec{v}_p,\vec{s}>}{\left | \vec{v}_p \right |\left | \vec{s} \right |}\frac{<\vec{s},\vec{r}_{\perp}>}{\left | \vec{s} \right |\left | \vec{r}_{\perp} \right |}\vec{r}_{\perp}$

 

[MaratZakirov]

 

[haruspex]

$m_p(\vec{v}_{p\parallel s} + \vec{v}_{p \perp s}) = m_p(\vec{v}_{p\parallel s} + \vec{v}_{p \perp s}) + m_c\vec{v}_c$

I have already explained twice that this equation is wrong. It ignores the reaction from the rail. Write the equation for conservation of momentum in the $\hat r$ direction only.

$\vec{v}_{p \parallel s \perp r}^1 = \vec{v}_{p \parallel s \perp r}$

I really do not know what that extended subscript notation means. Is it standard?
Would $\vec v_{\parallel x\parallel y}$ mean $(((\vec v.\hat x)\hat x).\hat y)\hat y$?

 

[Delta2]

2. I claim that perpendicular to s→ part of particle velocity will remain the same after collision

v→p⊥s=v→p⊥s1

EDIT: You may ignore this post, I just misunderstand your notation.

In my opinion it is the parallel to s component of the velocity of the particle that remains unchanged, assuming no friction between the sail and the particle. That is
$$\vec{v_{p\parallel s}}=\vec{v_{p\parallel s}}^1$$
However the parallel to s component of the velocity of the sail (that is of the car essentially since the sail is attached to car) is not conserved because there is the normal force from the rail, which has a component parallel to the sail. Also the normal force of the rail has a component perpendicular to the direction of the sail, which complicates things in order to write the equation for $\vec{v_{p\perp s}}$ and $\vec{v_{p\perp s}}^1$.

 

[haruspex]

In my opinion it is the parallel to s component of the velocity of the particle that remains unchanged

@MaratZakirov defined $\vec s$ as normal to the sail. Does that change your view?

 

[Delta2]

@MaratZakirov defined $\vec s$ as normal to the sail. Does that change your view?

Yes ok then it is the normal to $\vec{s}$ component that is conserved. (assuming no friction).

 

[MaratZakirov]

I have already explained twice that this equation is wrong. It ignores the reaction from the rail. Write the equation for conservation of momentum in the $\hat r$ direction only.I really do not know what that extended subscript notation means. Is it standard?
Would $\vec v_{\parallel x\parallel y}$ mean $(((\vec v.\hat x)\hat x).\hat y)\hat y$?

(I tried to edit my answer, but now I can not, so I make this post)

Yes, I agree, but I view on this in slightly different angle. Conservation of moment is always the case but in te $\vec{v}_{p \parallel s \perp r}$ direction there will be interaction with the planet Earth itself, so I claim that
$\vec{v}_{p \parallel s \perp r}^1 = -\vec{v}_{p \parallel s \perp r}$
do you agree?

Also (I must correct myself) remembering that $\vec s$ and $\vec r$ are unit vectors
$\vec{v}_{p \parallel s \perp r}=<\vec{v}_p,\vec{s}><\vec{s},\vec{r}_{\perp}>\vec{r}_{\perp}$
where $\vec{r}_{\perp}$ are perpendicular (any of two actually) to $\vec r$ unit vector
and <a, b> are obviously scalar product between $\vec a$ and $\vec b$ vectors. I do not know whether it is a standard notation or not, for me, it's pretty usable and as hope correct. My answer to your second question is yes, I meant exactly that.

 

[haruspex]

so I claim that
$\vec{v}_{p \parallel s \perp r}^1 = -\vec{v}_{p \parallel s \perp r}$
do you agree?

I see no reason to suppose that.
Consider the case where the particle strikes the sail square on. Your claim becomes
$\vec{v}_{p \perp r}^1 = -\vec{v}_{p \perp r}$.
I would claim that in this square on case the particle bounces back along the same line, so the ratio of $|\vec{v}_{p \perp r}|$ to $|\vec{v}_{p \parallel r}|$ is unchanged. It follows from those two that $\vec{v}_{p}^1 = -\vec{v}_{p}$, which is clearly false.

What you do have is
- conservation of momentum of particle parallel to the sail
- conservation of momentum of particle + cart parallel to the rail
- conservation of energy
and three unknowns
- final speed of cart
- final speed and direction of particle
There is no need to introduce any doubtful claims.

 

[pbuk]

What you do have is
- conservation of momentum of particle parallel to the sail
- conservation of momentum of particle + cart parallel to the rail
- conservation of energy
and three unknowns
- final speed of cart
- final speed and direction of particle
There is no need to introduce any doubtful claims.

Exactly this. And for heavens sake use the simple and obvious coordinate system with the rail stationary and on the x-axis, then you can remove all the $\parallel$ and $\perp$ subscripts and just talk about e.g. $v_{px}$ as the velocity of the particle parallel to the rail, and lots of terms disapper because you know that e.g. $v_{cy} = 0$ always.

(Edit: note that I referred to 'coordinate system' above rather than 'frame of reference' because I don't think you understand what that term means: in the FoR of the car the velocity of the car is always zero, by definition).

 

[MaratZakirov]

I would claim that in this square on case the particle bounces back along the same line

Please prove your statement, it is totally not obvious to me.

But I agree that fewer claims is better, so let's write equations without it:
1. Momentum conservation parallel to sail (no friction with sail)
$m_p\vec{v}_{p \perp s} = m_p\vec{v}_{p \perp s}^1$
2. Momentum conservation along rail
$m_p\vec{v}_{p \parallel r} = m_p\vec{v}_{p \parallel r}^1 + m_c\vec{v}_c$
3. Restricton
$<\vec{v}_c, \vec{r}_{\perp}> = 0$
4. Energy conservation
$m_p\left| \vec{v}_p \right|^2 = m_p\left|\vec{v}_p^1\right|^2 + m_c\left|\vec{v}_c\right|^2$

Do you agree with these 4 euations?

 

[MaratZakirov]

(Edit: note that I referred to 'coordinate system' above rather than 'frame of reference' because I don't think you understand what that term means: in the FoR of the car the velocity of the car is always zero, by definition).

I completely miss your point (https://en.wikipedia.org/wiki/Inertial_frame_of_reference)

Exactly this. And for heavens sake use the simple and obvious coordinate system with the rail stationary and on the x-axis, then you can remove all the and subscripts and just talk about e.g. as the velocity of the particle parallel to the rail, and lots of terms disapper because you know that e.g. always.

I do not see anything simple in simultaneously using two coordinate systems, one tied to the sail and other to the rail.
A solution in a system with a rail at rest must be obtained in a trivial way after this problem is solved.

 

[pbuk]

I completely miss your point (https://en.wikipedia.org/wiki/Inertial_frame_of_reference)

Yes, it is clear that you are missing the point so I will repeat it: the car/sail is not an intertial frame of reference because it is being accelerated by the particle and the rail.

I do not see anything simple in simultaneously using two coordinate systems, one tied to the sail and other to the rail.

Nobody is suggesting two coordinate systems. Just use one that is not being accelerated i.e. the rail.

A solution in a system with a rail at rest must be obtained in a trivial way after this problem is solved.

No, if you do manage to get a set of equations that work in the non-inertial frame of the sail/car then transforming them back into an intertial frame is not trivial.

There's no point asking for help in a forum and then ignoring the help you are given.

 

[MaratZakirov]

Yes, it is clear that you are missing the point so I will repeat it: the car/sail is not an intertial frame of reference because it is being accelerated by the particle and the rail.Nobody is suggesting two coordinate systems. Just use one that is not being accelerated i.e. the rail.No, if you do manage to get a set of equations that work in the non-inertial frame of the sail/car then transforming them back into an intertial frame is not trivial.

There's no point asking for help in a forum and then ignoring the help you are given.

Let's separate the patties from the flies.
The inertial frame of reference associated with the car before the collision is not accelerate. After the collision, the car will have a velocity different from $\vec{0}$ in this system.
Maybe you want to say that:
a) I didn't write equations correctly. (if so why?)
XOR
b) I can't write them correctly due to high complexity of case when I stick to car before collision. (if so why?)

 

[haruspex]

Please prove your statement, it is totally not obvious to me.

But I agree that fewer claims is better, so let's write equations without it:
1. Momentum conservation parallel to sail (no friction with sail)
$m_p\vec{v}_{p \perp s} = m_p\vec{v}_{p \perp s}^1$
2. Momentum conservation along rail
$m_p\vec{v}_{p \parallel r} = m_p\vec{v}_{p \parallel r}^1 + m_c\vec{v}_c$
3. Restricton
$<\vec{v}_c, \vec{r}_{\perp}> = 0$
4. Energy conservation
$m_p\left| \vec{v}_p \right|^2 = m_p\left|\vec{v}_p^1\right|^2 + m_c\left|\vec{v}_c\right|^2$

Do you agree with these 4 euations?

Yes, those are the correct equations.
In the square-on case, your equation 1 gives $m_p\vec{v}_{p \perp s} = m_p\vec{v}_{p \perp s}^1=0$. I.e., it bounces back along the same line.

 

[haruspex]

The inertial frame of reference associated with the car before the collision is not accelerate.

Yes, but previously you did not specify "before the collision". That's what has confused some commentators, me included. I realized that's what you probably meant a while back so stopped drawing attention to it.
Since the problem statement says the cart starts at rest, you are in fact using the ground frame, so why not say so?

 

[MaratZakirov]

Yes, but previously you did not specify "before the collision". That's what has confused some commentators, me included. I realized that's what you probably meant a while back so stopped drawing attention to it.
Since the problem statement says the cart starts at rest, you are in fact using the ground frame, so why not say so?

Let's look at my first post

All velocities are given for the inertial frame of reference associated with the cart before colliding with a particle

Maybe I should be more explicit?

 

[haruspex]

Let's look at my first post

Maybe I should be more explicit?

Ok, I missed that.

 

[pbuk]

Let's look at my first post

Maybe I should be more explicit?

I missed that too. You definitely do need to work on your communication skills, but rather than being explicit I think you should focus on expressing things simply and clearly. A little humility wouldn't hurt as well.

Since the problem statement says the cart starts at rest, you are in fact using the ground frame, so why not say so?

Exactly.