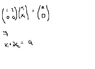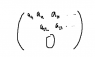Why Is the Rank of a Matrix Equal to Its Number of Pivot Points?

In summary, the rank of a matrix is equal to the number of pivot points in its reduced row echelon form. This is also true for any matrix that can be written as a product of an invertible matrix and its reduced row echelon form. The basis for the range of a matrix can be chosen as any combination of the columns with pivot points, as long as the last row is not a zero row. The range of a matrix is all the vectors that can be obtained by multiplying the matrix by any vector. The range is a subspace of the vector space that the matrix maps to.
  • #1
aaaa202
1,169
2
How come the rank of a matrix is equal to the amount of pivot points in the reduced row echelon form? My book denotes this a trivial point, but unfortunately I don't see it :(
 
Physics news on Phys.org
  • #2
How did you define "rank" in the first place?
 
  • #3
I don't what it is called in english but it's the dimension of the space that the linear function maps a vector onto.
 
  • #4
aaaa202 said:
I don't what it is called in english but it's the dimension of the space that the linear function maps a vector onto.

OK, so it's the dimension of the range. Good.

Next step: Take a matrix A. If we put it in reduced echelon form, then we obtain a matrix B. Do you see why both matrices have the same rank??

In general: if [itex]A=EBE^{-1}[/itex] for some invertible matrix E, do you see why A and B have the same rank?
 
  • #5
Okay yes, I should have been able to figure that out myself. But then suppose you have row reduced matrix like the one on the attached picture. As a basis for the range you choose the vectors equal to columns with pivot points -i.e. column 1,2,3. However - wouldn't it be just as good to choose 1,2 and 4? Since that'd also make a 3 pivot points.
And lastly: Would it then also work to choose any other combination of 3 vectors out of the 4?
 

Attachments

  • Unavngivet.png
    Unavngivet.png
    954 bytes · Views: 471
  • #6
aaaa202 said:
Okay yes, I should have been able to figure that out myself. But then suppose you have row reduced matrix like the one on the attached picture. As a basis for the range you choose the vectors equal to columns with pivot points -i.e. column 1,2,3. However - wouldn't it be just as good to choose 1,2 and 4? Since that'd also make a 3 pivot points.
And lastly: Would it then also work to choose any other combination of 3 vectors out of the 4?

Am I correct in saying that your last row is a zero row?? In that case, that doesn't count as a pivot point.
 
  • #7
Yes exactly. We have 3 pivots
 
  • #8
hmm I still don't get it tbh. Consider the matrix on the attached picture. What would a basis for the range then be? If you use the rule that the basis vectors equals the column with pivot points you'd get that (1,0) is a basis for the range. But how is (1,0) a basis for the solutions to equation x1 + 2x2 = a ?
 
  • #9
Can you give me a specific matrix?? I don't really understand your picture.

Do notice that the range is being generated by the columns of the matrix.
 
  • #10
oops the reason you didn't understand the picture was that i forgot to attach it: here
 

Attachments

  • Unavngivet.png
    Unavngivet.png
    2.4 KB · Views: 477
  • #11
In this case, the range will be all vectors of the form (a,0). So the rank will be 1.

Note that the range is generated by the column vectors: So the range = span (1,0) , (2,0) in this case.
 
  • #12
But isn't the range the solutions to the equation:
x1 + 2x2 = a
Why does x2 have to be 0?
 
  • #13
No, not at all. Given a matrix A, to find the range: you put up the equation Ax=y. All the possibilities for y constitute the range. That is: y is in the range if there is an x such that Ax=y.
 
  • #14
Ahh okay, it'd seem I didn't understand the basic definition of the range. But other than that I think I get it now.
Except! My real, deeper problem is perhaps that I don't understand why that, when you have a matrix like the one on the attached picture. How can you then be sure, that the columns with no pivot points can be written as a linear combination of the ones who do have pivot points? In general if you have n columns and n-a of them have pivots, how can you then know, that the a of them with no pivot points can be expressed as linear combinations of the n-a columns with pivots?
 

Attachments

  • Unavngivet.png
    Unavngivet.png
    2 KB · Views: 457
  • #15
If A is a linear transformation from vector space U to vector space V, then the range of A is a subspace of V, not U. It is the set of all vectors, y, in V, such that y= Ax for some x in A.
 

FAQ: Why Is the Rank of a Matrix Equal to Its Number of Pivot Points?

What is the definition of "rank" in a linear mapping?

The rank of a linear mapping is defined as the dimension of the vector space spanned by the images of the linear mapping. In other words, it is the number of linearly independent vectors in the range of the mapping.

How is the rank of a linear mapping related to its nullity?

The rank and nullity of a linear mapping are complementary. The nullity is the dimension of the null space of the mapping, which is the set of all vectors that are mapped to the zero vector. The rank-nullity theorem states that the sum of the rank and nullity is equal to the dimension of the domain of the mapping.

Why is the rank of a linear mapping important?

The rank of a linear mapping provides important information about the behavior of the mapping. It can determine whether the mapping is injective (one-to-one), surjective (onto), or bijective (both one-to-one and onto). The rank also plays a role in solving systems of linear equations and in computing determinants.

How is the rank of a linear mapping affected by elementary row operations?

The rank of a linear mapping is not affected by elementary row operations, which include multiplying a row by a nonzero constant, interchanging two rows, and adding a multiple of one row to another. These operations only change the representation of the mapping, but the rank remains the same.

Can the rank of a linear mapping be greater than the dimensions of its domain and range?

Yes, the rank of a linear mapping can be greater than the dimensions of its domain and range. This occurs when the mapping is not a square matrix, meaning the number of rows and columns are not equal. In this case, the rank is limited by the smaller dimension, but it can still be greater than the dimensions of both the domain and range.

Similar threads

MHB Check the statements about a 4x5 matrix with rank 2.
Replies
9
Views
4K
I Preserving Rank: Exploring Elementary Operations in Matrix Algebra
Replies
4
Views
1K
I Dimension and solution to matrix-vector product
Replies
4
Views
2K
Test Tomorrow Linear independence, spanning, basis
Replies
7
Views
2K
MHB Finding the Rank and Basis for a matrix
Replies
4
Views
2K
I Row space, Column space, Null space & Left null space
Replies
8
Views
2K
MHB How to Quickly Find the Rank of a 4 x 6 Matrix Using Column Operations
Replies
2
Views
2K
MHB How can I prove the rank of a matrix with a specific pattern of entries?
Replies
2
Views
1K
Codomain and Range of Linear Transformation
Replies
10
Views
2K
I About permutation acting on the Identity matrix
Replies
7
Views
1K

Hot Threads

Recent Insights

Back
Top