MHB Rank One Tensors .... Fortney Appendix A, Section A2 ....

[Math Amateur]

I am reading Jon Pierre Fortney's book: A Visual Introduction to Differential Forms and Calculus on Manifolds ... and am currently focused on Appendix A : Introduction to Tensors ...I need help to understand some statements/equations by Fortney concerning rank one tensors ...

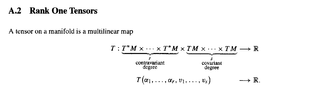
Those remarks by Fortney read as follows:
View attachment 8786
View attachment 8787In the above text by Fortney we read the following:

" ... ... Suppose we change the coordinates from $$(x^1, x^2, \ ... \ ... \ , x^n )$$ to $$(u^1, u^2, \ ... \ ... \ , u^n )$$ using the $$n$$ functions

$$u^1 (x^1, x^2, \ ... \ ... \ , x^n ) = u_1 $$

$$u^2 (x^1, x^2, \ ... \ ... \ , x^n ) = u_2$$

... ...

... ...

$$u^n (x^1, x^2, \ ... \ ... \ , x^n ) = u_n$$ ... ... "

My question is as follows:

What do the equations $$u^i (x^1, x^2, \ ... \ ... \ , x^n ) = u_i$$ mean ... ? ... how do we interpret them ...?

What would it mean for example if we wanted to form the differentials $$du^i$$ ... ?Help will be appreciated ...

Peter
EDIT ... Reflecting on the above ... a further question ... are the coordinate functions $$ (x^1, x^2, \ ... \ ... \ , x^n )$$ essentially a basis for M ... (I am assuming the manifold is a vector space ... hmmm bt not sure it is ...?)

Hope someone can clarify ...

Peter

 

[I like Serena]

What do the equations $$u^i (x^1, x^2, \ ... \ ... \ , x^n ) = u_i$$ mean ... ? ... how do we interpret them ...?

Hi Peter,

It means that $u_1$ is a function $\mathbb R^n \to \mathbb R$.
And $(u^1,\ldots,u^n)$ is an element of $\mathbb R^n$, just like $(x^1,\ldots,x^n)$.
The function $u_1$ maps $(x^1,\ldots,x^n)$ to $u^1$.

I'm not sure if you're already familiar with the concept of charts. Are you?
The concept is similar to the charts that we have in an atlas of the earth.
The surface of the Earth represents the manifold. And a chart represents a page with a map of a section of the earth.

In this case it means that we have two overlapping charts, let's call them $\phi$ and $\psi$, that map a subset of $M$ to $\mathbb R^n$.
The chart $\phi$ would map a point $p$ in $M$ to $(x^1,\ldots,x^n)$, which is one set of local coordinates.
And $\psi$ would map $p$ to $(u^1,\ldots,u^n)$, which is another set of coordinates for the same point, but in a different chart.

What would it mean for example if we wanted to form the differentials $$du^i$$ ... ?

$du^i$ is a function $T_pM\to \mathbb R$ just like $dx^i$, where $T_p M$ is the so called tangent space of $M$ at a point $p$.
However, since both $M$ and $T_p M$ are abstract spaces, we need more abstractions to map them to each other properly.

are the coordinate functions $$ (x^1, x^2, \ ... \ ... \ , x^n )$$ essentially a basis for M ... (I am assuming the manifold is a vector space)

$M$ is a manifold, which means that it is locally isomorphic to Euclidean space $\mathbb R^n$.
It means that $M$ can be a vector space, but that this is not necessarily the case.
So we can not assume that.
If $M$ would be a vector space, it would be globally isomorphic to Euclidean space.

We can say however that $T_p M$, the tangent space of $M$ at point $p$, is a vector space.

The point $(x^1,\ldots,x^n) \in \mathbb R^n$ is a representation of a point $p \in M$ according to a local chart.
If $M$ would be the vector space $\mathbb R^n$, then we might pick the identity function as a local chart.
Then $(x^1,\ldots,x^n)$ would simply be a point in $M$.
It's just that a manifold is an abstraction of this.

 

[Math Amateur]

Hi Peter,

It means that $u_1$ is a function $\mathbb R^n \to \mathbb R$.
And $(u^1,\ldots,u^n)$ is an element of $\mathbb R^n$, just like $(x^1,\ldots,x^n)$.
The function $u_1$ maps $(x^1,\ldots,x^n)$ to $u^1$.

I'm not sure if you're already familiar with the concept of charts. Are you?
The concept is similar to the charts that we have in an atlas of the earth.
The surface of the Earth represents the manifold. And a chart represents a page with a map of a section of the earth.

In this case it means that we have two overlapping charts, let's call them $\phi$ and $\psi$, that map a subset of $M$ to $\mathbb R^n$.
The chart $\phi$ would map a point $p$ in $M$ to $(x^1,\ldots,x^n)$, which is one set of local coordinates.
And $\psi$ would map $p$ to $(u^1,\ldots,u^n)$, which is another set of coordinates for the same point, but in a different chart.
$du^i$ is a function $T_pM\to \mathbb R$ just like $dx^i$, where $T_p M$ is the so called tangent space of $M$ at a point $p$.
However, since both $M$ and $T_p M$ are abstract spaces, we need more abstractions to map them to each other properly.
$M$ is a manifold, which means that it is locally isomorphic to Euclidean space $\mathbb R^n$.
It means that $M$ can be a vector space, but that this is not necessarily the case.
So we can not assume that.
If $M$ would be a vector space, it would be globally isomorphic to Euclidean space.

We can say however that $T_p M$, the tangent space of $M$ at point $p$, is a vector space.

The point $(x^1,\ldots,x^n) \in \mathbb R^n$ is a representation of a point $p \in M$ according to a local chart.
If $M$ would be the vector space $\mathbb R^n$, then we might pick the identity function as a local chart.
Then $(x^1,\ldots,x^n)$ would simply be a point in $M$.
It's just that a manifold is an abstraction of this.

Thanks Klaas ... for an extremely helpful post ...

... and yes ... familiar (but not confident...) with concept of charts ...

Peter