greg_rack
Gold Member
- 361
- 79
Howdy guys,
Say we have been given the four thin-walled cross sections below loaded in pure torsion, where the material in black, titanium, has E=100GPa and the one grey one, aluminum, E=75GPa(no clue why Es are given, as I would have expected the shear modulus, G... maybe it is expected to use the equation G=##f(v, E)## to derive the latter).
But anyways, the point now would be to rank by eye each one of them once from the stiffest to the less stiff cross section, and then from the strongest to the weakest.
As the "by eye" might have led you to think, a reasoning is expected in place of numbers/ratios(or a maybe a more wordy version of the latter) to justify the resulting ranking.
Therefore, I would be curious to see how you guys would reason such an exercise and see the thought process behind a reasonable ranking. For the bi-material strips specifically, I really wouldn't know how to tackle this without relying on the bookkeeping process of:
-torques superposition, ##T=T_1+T_2##;
-compatibility equation for the deflection rate to be equal in both parts of the cs, ##\frac{d\theta}{dz}=\frac{3T_1}{G_1s_1t^3}=\frac{3T_2}{G_2s_2t^3}##
-solving for the individual torques and then computing the individuals ##\tau_{max}## and ##\frac{d\theta}{dz}##
Any ideas? :)
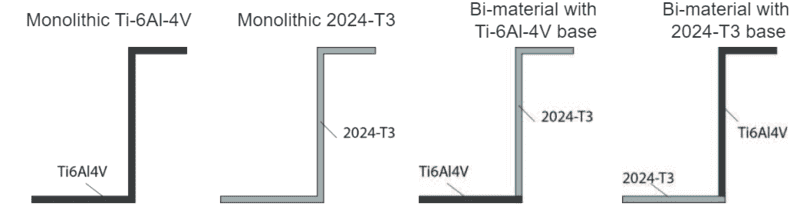
Say we have been given the four thin-walled cross sections below loaded in pure torsion, where the material in black, titanium, has E=100GPa and the one grey one, aluminum, E=75GPa(no clue why Es are given, as I would have expected the shear modulus, G... maybe it is expected to use the equation G=##f(v, E)## to derive the latter).
But anyways, the point now would be to rank by eye each one of them once from the stiffest to the less stiff cross section, and then from the strongest to the weakest.
As the "by eye" might have led you to think, a reasoning is expected in place of numbers/ratios(or a maybe a more wordy version of the latter) to justify the resulting ranking.
Therefore, I would be curious to see how you guys would reason such an exercise and see the thought process behind a reasonable ranking. For the bi-material strips specifically, I really wouldn't know how to tackle this without relying on the bookkeeping process of:
-torques superposition, ##T=T_1+T_2##;
-compatibility equation for the deflection rate to be equal in both parts of the cs, ##\frac{d\theta}{dz}=\frac{3T_1}{G_1s_1t^3}=\frac{3T_2}{G_2s_2t^3}##
-solving for the individual torques and then computing the individuals ##\tau_{max}## and ##\frac{d\theta}{dz}##
Any ideas? :)