Rate of Change of Plane's Distance from Radar Station - Gina's Question

[MarkFL]

Here is the question:

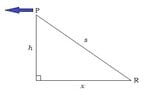
related rates; Find the rate at which the distance from the plane to the station is increasing when it is..?


A plane flying horizontally at an altitude of 1 mi and a speed of 470 mi/h passes directly over a radar station. Find the rate at which the distance from the plane to the station is increasing when it is 5 mi away from the station. (Round your answer to the nearest whole number.)
__ mi/h

thanks will vote best answer!

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello Gina,

First, let's draw a diagram:

View attachment 1445

The plane is at $P$, the radar station is at $R$, $h$ is the altitude of the plane (which is constant since its flight is said to be horizontal) and $x$ is the distance from the radar station to the point on the ground (or at the same level as the radar station) directly below the plane. $s$ is the distance from the plane the the radar station.

Using the Pythagorean theorem, we may state:

(1) \(\displaystyle x^2+h^2=s^2\)

Implicitly differentiating (1) with respect to time $t$, we find:

\(\displaystyle 2x\frac{dx}{dt}=2s\frac{ds}{dt}\)

We are interested in solving for \(\displaystyle \frac{ds}{dt}\) since we are asked to find the rate at which the distance from the plane to the station is increasing when it is 5 mi away from the station. So, we find:

\(\displaystyle \frac{ds}{dt}=\frac{x}{s}\frac{dx}{dt}\)

Now, we do not know $x$ but we know $h$ and $s$, and so solving (1) for $x$ (and taking the positive root since it represents a distance), we find:

\(\displaystyle x=\sqrt{s^2-h^2}\)

And so we have:

\(\displaystyle \frac{ds}{dt}=\frac{\sqrt{s^2-h^2}}{s}\frac{dx}{dt}\)

Now, the speed $v$ of the plane represents the time rate of change of $x$, hence:

\(\displaystyle v=\frac{dx}{dt}\)

and so we may write:

\(\displaystyle \frac{ds}{dt}=\frac{v\sqrt{s^2-h^2}}{s}\)

Now, we may plug in the given data:

\(\displaystyle v=470\frac{\text{mi}}{\text{hr}},\,s=5\text{ mi},\,h=1\text{ mi}\)

and we then find:

\(\displaystyle \frac{ds}{dt}=\frac{470\sqrt{5^2-1^2}}{5} \frac{\text{mi}}{\text{hr}}=188\sqrt{6}\frac{\text{mi}}{\text{hr}}\approx460.504071643238 \text{ mph}\)

And so we have found that the rate at which the distance from the plane to the station is increasing when it is 5 mi away from the station is about 461 mph.