- #1
emtae55
- 24
- 0
When we measure 'the rate of conduction heat transfer'=Q , we assume that the hot side and the cold side's area are same. But if the both side's area is different to each other, how can i know the rate of conduction heat transfer?
like below figure.
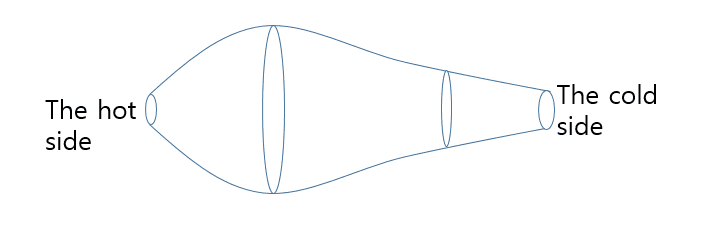

Would you like to help me?? Thanks.
like below figure.
Would you like to help me?? Thanks.
Last edited: