Ratio of the area of triangle in terms of another triangle

[mathlearn]

:D I have trouble in determining the ratio of the area of $\triangle PST$ in terms of $\triangle PQR$

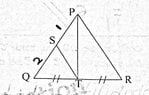
In the triangle PQR $QT=TR$, $PS=1 cm$ , $SQ=2 cm$ , How should I be writing the area of $\triangle PST$ in terms of $\triangle PQR $

View attachment 6031

What is known by me :

Since $|\overline{QT}|=|\overline{TR}|$ it follows that $\triangle PQT$ and $\triangle PTR$ have equal areas, so $$[PQT]=\frac12[PQR]$$

Has It got to do something with,

If two polygons are similar, the ratio of their areas is equal to the square of the ratio of their corresponding sides.

So what must be done from here?

 

[Euge]

Hi mathlearn,

A key idea is that $\triangle PST$ and $\triangle PQT$ share the same altitude from vertex $T$. Using this fact, deduce that $\operatorname{Area}(\triangle PST) = \frac{1}{3}\operatorname{Area}(\triangle PQT)$.

 

[mathlearn]

Hi mathlearn,

A key idea is that $\triangle PST$ and $\triangle PQT$ share the same altitude from vertex $T$. Using this fact, deduce that $\operatorname{Area}(\triangle PST) = \frac{1}{3}\operatorname{Area}(\triangle PQT)$.

Hi Euge ;) ,

What I still don't understand is that ,

How did $\operatorname{Area}(\triangle PST) = \frac{1}{3}\operatorname{Area}(\triangle PQT)$ get derived?

From $|\overline{PS}|=\frac12|\overline{SQ}|$ it follows that the area of $\triangle PST$ is a half of the area of $\triangle PQT$ , From there I don't get it that much

 

[MarkFL]

I would use this formula for the area $A$ of a triangle:

$$A=\frac{1}{2}ab\sin(C)$$

To derive the relationship Euge mentioned. :)

 

[mathlearn]

I would use this formula for the area $A$ of a triangle:

$$A=\frac{1}{2}ab\sin(C)$$

To derive the relationship Euge mentioned. :)

:) Thanks but the issue is I don't know the use of this formula

 

[MarkFL]

Draw a line from $S$ to $\overline{PT}$ parallel to $\overline{QT}$ and use similarity...:D

 

[Euge]

Hi Euge ;) ,

What I still don't understand is that ,

How did $\operatorname{Area}(\triangle PST) = \frac{1}{3}\operatorname{Area}(\triangle PQT)$ get derived?

From $|\overline{PS}|=\frac12|\overline{SQ}|$ it follows that the area of $\triangle PST$ is a half of the area of $\triangle PQT$ , From there I don't get it that much

Hey mathlearn,

I suggested that you deduce this from the fact that $\triangle PST$ and $\triangle PQT$ share the same altitude from vertex $T$. Suppose their common altitude is $h$. Since the area of a triangle is $\dfrac{1}{2}\times (\text{base})\times (\text{height})$, then $\operatorname{Area}(\triangle PQT) = \dfrac{1}{2}(3)(h)$ and $\operatorname{Area}(\triangle PST) = \dfrac{1}{2}(1)(h)$. From here you can see how the result is derived.