- #1
Saitama
- 4,243
- 93
Homework Statement
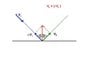
A light ray parallel to the x-axis strikes the outer reflecting surface of a sphere at a point (2,2,0). Its center is at the point (0,0,-1). The unit vector along the direction of reflected ray is ##x\hat{i}+y\hat{j}+z\hat{k}##. Find the value of ##yz/x^2##.
Homework Equations
The Attempt at a Solution
The vector for the light ray traveling parallel to x-axis is ##-2\hat{i}##. The incident ray and the reflected ray make equal angle with the normal passing through (2,2,0). The vector associated with the normal at (2,2,0) is ##-2\hat{i}-2\hat{j}-\hat{k}##.
Dot product of the incident ray and normal:
[tex]4=2\times 3 \cos \theta \Rightarrow \cos\theta = \frac{2}{3}[/tex]
where ##\theta## is the angle between the normal and incident ray.
Dot product of reflected and incident ray:
[tex]-2x=2\cos 2\theta \Rightarrow x=\frac{1}{9}[/tex]
Dot product of normal and reflected ray:
[tex]-2x-2y-z=3\cos \theta \Rightarrow 2y+z=\frac{-20}{9}[/tex]
I still need one more equation.
Any help is appreciated. Thanks!