member 731016
- Homework Statement
- Please see below
- Relevant Equations
- Please see below
For this problem,
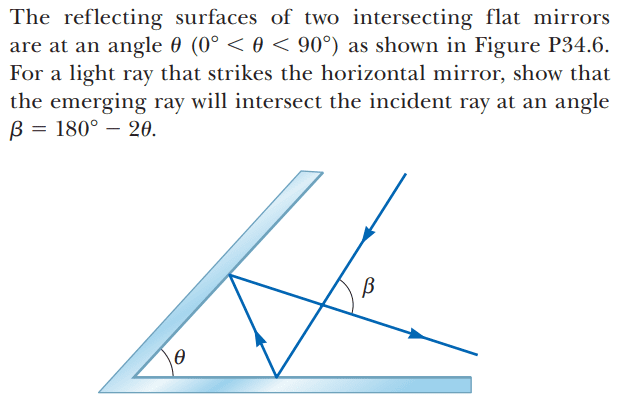
The solution is,
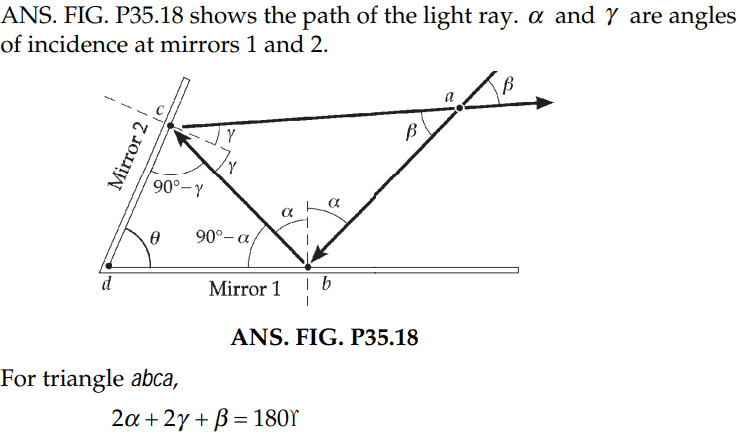

I don't understand how if ## \gamma < 0## then there will be multiple reflections? I don't understand how ##\gamma## can be negative.
Many thanks!
The solution is,
I don't understand how if ## \gamma < 0## then there will be multiple reflections? I don't understand how ##\gamma## can be negative.
Many thanks!