Re: location of maximum stresses

[paddles069]

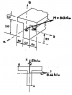
With respect to upper figure in the attached diagram, I don't really understand how the moment acts on the beam. I've always understood moments as forces that cause rotation and so when it is drawn as a straight line in the upper figure I'm not sure how that is affecting the beam.

With regards to the lower figure, the solutions state that 'by inspection', the maximum tensile stress is located at point B and the maximum compressive stress is located at point C. Why is this? How do they arrive at this conclusion?

 

[SteamKing]

The moment in the upper figure is shown resolved into its two components in the lower figure (notice the moments shown on the y and z axes). In effect, the beam is being bent about the y and z axes at the same time.

 

[Jupiter6]

It's an understandable question. Treat it as any other beam cross-section, except it's being twisted to the right and twisted upwards, as opposed to a straight on load.

To answer your questions:
Moments are a force applied at a distance from some center. They don't have to cause a rotation and if this is the case, they can be resolved into forces applied, at a certain distance.

I too was thrown off by a lot of these things in sophomore solid mechanics because they were never related to the real world.

Their "by inspection" statement assumes you are familiar with beam cross sections. In cases of T-beams, I think you should treat them as I-beams when "inspecting".

First and foremost, always draw your freebody diagrams or break the problem down into FBD's. Always!

 

[pongo38]

I think the M should have had a double headed arrow, indicating a moment about the axis with the arrow head at its end. In a 3-dimensional sketch, can you sketch the stress distributions separately from the two components? This is how you can see by inspection the quality of the stresses at B and at C.

 

[DeeNos]

I would like to address your questions regarding the location of maximum stresses in the attached diagram.

Firstly, it is important to understand that a moment is a rotational force that acts on a body. In the case of the beam, the moment acts at a distance from the support, causing a bending effect on the beam. This bending effect creates stresses within the beam, which can be both tensile and compressive.

In the upper figure, the moment is represented as a straight line because it is acting perpendicular to the plane of the diagram. This does not mean that it is not affecting the beam. In fact, the moment is causing a bending moment and therefore, stresses within the beam.

Moving on to the lower figure, the statement 'by inspection' means that the solution can be determined by simply looking at the diagram. This is because the moment is acting at a distance from the support, causing a bending effect on the beam. As a result, the top of the beam experiences tensile stresses, while the bottom experiences compressive stresses. Therefore, the maximum tensile stress will be located at the point B, which is the furthest point from the neutral axis, and the maximum compressive stress will be located at point C, which is closest to the neutral axis.

To further understand how this conclusion is reached, it is important to consider the concept of the neutral axis. This is an imaginary line within the beam where there is no bending or stress. As we move away from the neutral axis, the bending moment increases, resulting in higher stresses. This is why the maximum tensile stress is located at the furthest point from the neutral axis (point B) and the maximum compressive stress is located at the closest point to the neutral axis (point C).

I hope this explanation helps clarify your doubts. As a scientist, it is important to understand the fundamental principles and concepts behind any solution or conclusion, rather than just accepting it 'by inspection'. I would encourage you to further explore the concept of bending moments and neutral axis to gain a deeper understanding of this topic.