- #1
PhysicsKT
- 17
- 0
Homework Statement
Three ants A, B and C are crawling on a large horizontal tabletop always occupying vertices of an equilateral triangle, size of which may vary with time. If at an instant, speeds of A and B are vA and vB, prove that vC>= vA+vB.
Homework Equations
Well, that's what I don't understand- to always maintain the shape of an equilateral triangle, one of the paths they may acquire is constantly approach each other.
The Attempt at a Solution
First I considered them to move along the equilateral triangle- but using cosine law doesn't help. If they approach each other, I got the relation that their velocities must be equal since:
We write the
What to do now in order to make a solid conclusion?
Attachments
-
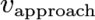 4a1c36cfa75b7d70a6a701443f639f9696878c19.png638 bytes · Views: 1,142
4a1c36cfa75b7d70a6a701443f639f9696878c19.png638 bytes · Views: 1,142 -
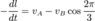 118d0a979dca63220dfb2aa8ee831f436199f443.png1.7 KB · Views: 1,070
118d0a979dca63220dfb2aa8ee831f436199f443.png1.7 KB · Views: 1,070 -
 615aef1b18eabbe4a8ddbf06b63e99a32b41771c.png660 bytes · Views: 1,176
615aef1b18eabbe4a8ddbf06b63e99a32b41771c.png660 bytes · Views: 1,176 -
 a069a777b9f40e4658e1c2be3a4b82efa4bdf7ac.png1.4 KB · Views: 1,123
a069a777b9f40e4658e1c2be3a4b82efa4bdf7ac.png1.4 KB · Views: 1,123 -
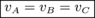 071889d7187677595a6673b5034b67e84aaa019f.png797 bytes · Views: 1,105
071889d7187677595a6673b5034b67e84aaa019f.png797 bytes · Views: 1,105