Really on simple energy and spring on incline

[B-80]

A 2.00 kg block is placed against a spring on a frictionless 30.0° incline (Fig. 8-33). (The block is not attached to the spring.) The spring, whose spring constant is 19.6 N/cm, is compressed 16.0 cm and then released.

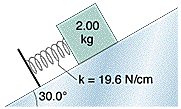
(a) What is the elastic potential energy of the compressed spring?
So I think of it like this, it wants the answer in joules, so I convert 19.6N/cm to .196N/m, and 16cm to .16m anyway. PE=1/2 K X^2
so
PE=.5(.196)(.16^2) = .0025088J but it's wrong. I know this is very simple, But I don't understand why I am wrong here

 

[hage567]

so I convert 19.6N/cm to .196N/m

This is wrong. Try again, make sure your units work out.

 

[B-80]

I tried leaving them the same, but that didn't work either. The only other thing I can think of is leaving one the same and changing the other, which is mixing units, and that's wrong. What is wrong about it, can you be a little more specific?

 

[hage567]

You just didn't convert it properly. Write it out so you can see how the units need to be:

19.6 N/cm * 100 cm/m = 1960 N/m.

 

[B-80]

Ahh thank you, I swear I lose so many points because of stuff like this