- #1
Dr_Pill
- 41
- 0
I got a bunch of questions about reciprocal lattice, I start with this one:
In an x-ray experiment:
For one specific orientation of your incident beam on your real lattice, only a portion of the points of your reciprocal lattice will become visible as your diffraction pattern right?
See my picture
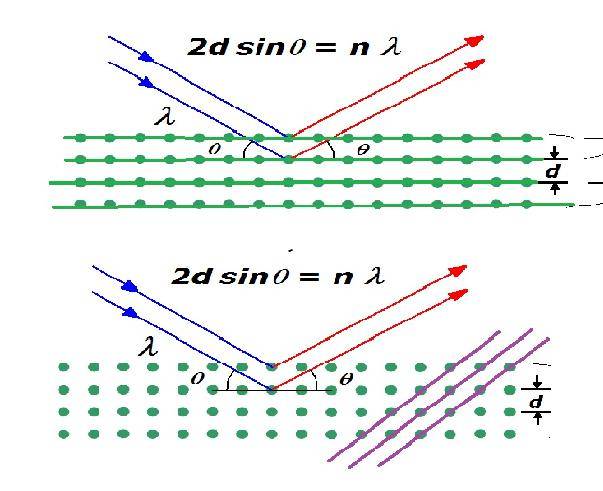
For one incident beam, only the parallel planes are involved in your diffraction and so only the reciprocal lattice points that represent these set of parallel planes will becoem visible on your diffraction pattern
If you want to make other reciprocal points points visible on your diffraction pattern, u have to change the orientation of your incident beam so that another set of parallel planes is involved in diffraction
So in first picture, your blue beam will get the reciprocal points that representing the green parallel planes visible on your diffraction pattern.
Second picture, the same blue beam does nothing on the purple planes, so the reciprocal points that represents the purple planes will not be visible on the diffraction pattern.
Is this correct?
In an x-ray experiment:
For one specific orientation of your incident beam on your real lattice, only a portion of the points of your reciprocal lattice will become visible as your diffraction pattern right?
See my picture
For one incident beam, only the parallel planes are involved in your diffraction and so only the reciprocal lattice points that represent these set of parallel planes will becoem visible on your diffraction pattern
If you want to make other reciprocal points points visible on your diffraction pattern, u have to change the orientation of your incident beam so that another set of parallel planes is involved in diffraction
So in first picture, your blue beam will get the reciprocal points that representing the green parallel planes visible on your diffraction pattern.
Second picture, the same blue beam does nothing on the purple planes, so the reciprocal points that represents the purple planes will not be visible on the diffraction pattern.
Is this correct?
Last edited: