Rectangular Box with two non zero potential faces

AI Thread Summary
To solve the problem of a rectangular box with two non-zero potential faces, the approach involves finding the potential at each end face and applying the superposition principle for the net potential. There is confusion regarding the boundary condition, particularly with the presence of an exponential term when x equals l. It is suggested that using (l-x) as a coordinate can simplify the solution and potentially eliminate the exponential term. The discussion also touches on using hyperbolic functions like sinh and cosh for a more aesthetically pleasing solution. The final inquiry confirms the correctness of applying the hyperbolic cosine function in a three-dimensional context.
guyvsdcsniper
Messages
264
Reaction score
37
Homework Statement
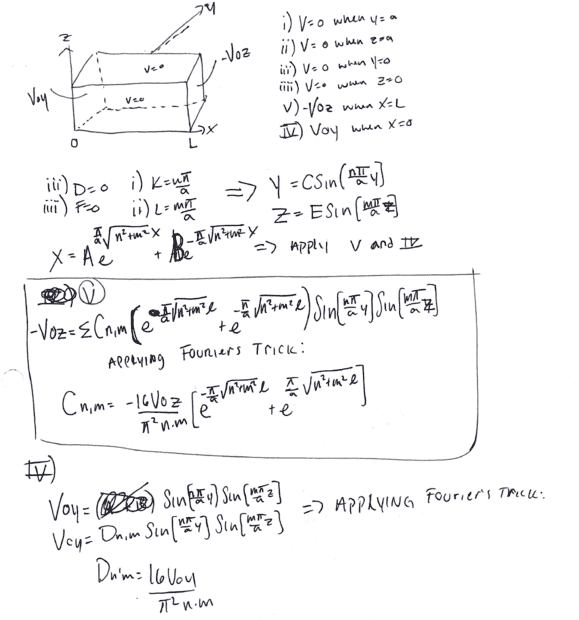
a conducting rectangular hollow box has zero potential on all its rectangular sides and a potential of
Voy at x=0 and -Voz at x=l

Find the potential inside
Relevant Equations
laplace's equation
I believe what I have to do to solve this problem is find the potential at each end face and then use the super position principle to find the net potential. So my boundary condition v and iv will give the potential at each respective position.
Im just a bit confused about my boundary V.

Usually when doing these problems the condition causes a coefficient to be zero. Here we have a potential when x=l
So i get this big ugly exponential attached to my coefficient.

Does this seem correct

Screen Shot 2022-05-05 at 8.19.15 AM.png
 
Physics news on Phys.org
Yes, generally you will get some sort of exponential attached. You could get rid of it (should you wish to do so) by using (l-x) as a coordinate for that part of the solution rather than x. (Also, you may find it more aesthetically pleasing to use sinh and cosh instead of the exponential functions.)

On a completely different note: The Roman number 6 is written VI while IV is the Roman number 4.
 
Orodruin said:
Yes, generally you will get some sort of exponential attached. You could get rid of it (should you wish to do so) by using (l-x) as a coordinate for that part of the solution rather than x. (Also, you may find it more aesthetically pleasing to use sinh and cosh instead of the exponential functions.)

On a completely different note: The Roman number 6 is written VI while IV is the Roman number 4.
Ohh that is write I can write the exponential as for condition V as 2cosh(x).

so then I would get 2cosh(l-x)?
 
Yes, although you can absorb the 2 into the coefficient.
 
Orodruin said:
Yes, although you can absorb the 2 into the coefficient.
I did something similar to this in a 2-D laplace equation but now that it is 3-D the exponential is raised to a half power, π/a√(n2+m2)(l-x)
So then I would have Cosh(π/a√(n2+m2)(l-x))

Is that correct?
 
Thread 'Minimum mass of a block'

Thread 'Minimum mass of a block'

Here we know that if block B is going to move up or just be at the verge of moving up ##Mg \sin \theta ## will act downwards and maximum static friction will act downwards ## \mu Mg \cos \theta ## Now what im confused by is how will we know " how quickly" block B reaches its maximum static friction value without any numbers, the suggested solution says that when block A is at its maximum extension, then block B will start to move up but with a certain set of values couldn't block A reach...
View full post »
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Understanding a math step in solving Schrödinger's equation for single particle in a box
Replies
8
Views
904
Ion moving through electric potential difference and magnetic field
Replies
8
Views
1K
Minimizing the Energy of Two Conductors Very Far Apart
Replies
23
Views
1K
Find potential within a pipe using Laplace's equation
Replies
18
Views
2K
Evaluating the boundary conditions for a rectangular pipe
Replies
19
Views
2K
Electrostatic Potential in a Box
Replies
1
Views
2K
Correct Setup for Finite Difference to Calculate Quantum Tunneling
Replies
2
Views
916
Why can we move the spring with constant speed when we apply a force?
Replies
29
Views
2K
How electric potential boundary condition works
Replies
5
Views
3K
Electric Potential inside an insulating sphere
Replies
11
Views
5K

Hot Threads

Recent Insights

Back
Top