Reducing one algebraic fraction to another

[brotherbobby]

Homework Statement

If $$\frac{x}{l(mb+nc-la)}= \frac{y}{m(nc+la-mb)}=\frac{z}{n(la+mb-nc)},$$
prove that $$\boxed{\frac{l}{x(by+cz-lz)}= \frac{m}{y(cz+ax-by)}=\frac{n}{z(ax+by-cz)}}$$

Relevant Equations

A theorem on algebraic fractions :
(1) If $\frac{a}{b}= \frac{c}{d}\Rightarrow \frac{ax}{bx}=\frac{cy}{dy}$
(2) If $\frac{a}{b}=\frac{c}{b}=\frac{e}{f}=\ldots$, each of the fractions is equal to $\pmb{\left(\frac{pa^n+qc^n+re^n+\dots}{pb^n+qd^n+rf^n+\ldots}\right)^{\frac{1}{n}}}$, where variables $p, q, r,\ldots, n\in \mathbb{R}$

Problem statement : Let me copy and paste the problem as it appears in the text :

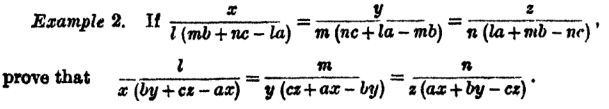
Attempt : I am afraid this looks like a very difficult problem, despite being at the elementary level (high school). My glance through the text shows that the authors have gone about reducing the first set of fractions to the second directly, without making the (traditional) use of the auxilliary variable $k$ to which the whole of the first list is first equated to and then simplified. Let me go with this method.

Let the given list of fractions $\frac{x}{l(mb+nc-la)}= \frac{y}{m(nc+la-mb)}=\frac{z}{n(la+mb-nc)}=\boldsymbol{k}\;\text{(say)}$.

This would yield $x = kl(mb+nc-la),\, y = km(nc+la-mb)\,\text{and}\, z = kn(la+mb-nc)$.

Let me the take first term in what I have to prove (given above), viz. $\frac{l}{x(by+cz-lz)}$.

Sunstituting for $x, y, z$ from above in terms of $k, l, m, n, a, b, c$, we get :
$$\text{L.H.S (Term 1)} = \frac{l}{x(by+cz-lz)} = \frac{l}{\underbrace{kl(mb+nc-la)}_{x}\left[ b\underbrace{km(nc+la-mb)}_{y}+c\underbrace{kn(la+mb-nc)}_{z}-a\underbrace{kl(mb+nc-la)}_{x} \right]},$$
$$=\frac{1}{k^2(mb+nc-la)\left[mnbc+\bcancel{lmab}-m^2b^2+\cancel{lnac}+mnbc-n^2c^2-\bcancel{lmab}-\cancel{lnac}+la^2 \right]},$$
$$=\frac{1}{k^2(mb+nc-la)(2mnbc+l^2a^2-m^2b^2-n^2c^2)},$$
$$=\frac{1}{k^2(\cancel{2m^2nb^2c}+l^2ma^2b-m^3b^3-\bcancel{mn^2bc^2}+\bcancel{2mn^2bc^2}+l^2na^2c-\cancel{m^2nb^2c}-n^3c^3-2lmnabc-l^3a^3+lm^2ab^2+ln^2ac^2)},$$
$$=\frac{1}{k^2(m^2nb^2c+l^2ma^2b-m^3b^3+mn^2bc^2+l^2n^2c-n^3c^3-2lmnabc-l^3a^3+lm^2ab^2+ln^2ac^2)}$$
and, upon rearranging, the first rational term on the L.H.S. reduces to :
$$\small{\text{L.H.S (Term 1)} = \frac{l}{x(by+cz-lz)}=\frac{1}{k^2(l^2ma^2b+lm^2ab^2+l^2na^2c+ln^2ac^2+m^2nb^2c+mn^2bc^2-l^3a^3-m^3b^3-n^3c^3-2lmnabc)}}$$... (1)

Let me take the second term of what I have to prove (given above), viz. $\frac{m}{y(cz+ax-by)}$, substitute for $x,y,z$ like before and see if the final expression matches the same final expression of that above.

$$\text{L.H.S (Term 2)}= \frac{m}{y(cz+ax-by)}=\frac{1}{k^2(nc+la-mb)\left[ cn(la+mb-nc)+al(mb+nc-la)-bm(nc+la-mb)\right]},$$
$$=\frac{1}{k^2(nc+la-mb)(lnac+\cancel{mnbc}-n^2c^2+\bcancel{lmab}+lnac-l^2a^2-\cancel{mnbc}-\bcancel{lmab}+m^2b^2)},$$
$$=\frac{1}{k^2(nc+la-mb)(2lnac-l^2a^2+m^2b^2-n^2c^2)},$$
$$=\frac{1}{k^2(\cancel{2ln^2ac^2}-\bcancel{l^2na^2c}+m^2nb^2c-n^3c^3+\bcancel{2l^2na^2c}-l^3a^3+lm^2ab^2-\cancel{ln^2ac^2}-2lmnabc+l^2ma^2b-m^3b^3+mn^2bc^2)},$$
$$=\frac{1}{k^2(l^2ma^2b+lm^2ab^2+m^2nb^2c+mn^2bc^2+l^2na^2c+ln^2ac^2-l^3a^3-m^3b^3-n^3c^3-2lmnabc)},$$

which is the same found above (1) when the first term was reduced.

The third fraction, viz. $\frac{n}{z(ax+by-cz)}$ also reduces to the same expression as (1) above, as I have checked.

Doubt : So I did the problem. However, as you have noticed, I have made use of the auxilliary variable $k$ above, which I equated all the fractions to. Does anyone know a way by which the fractions given can be directly reduced to those required? (That is the method asked for by the authors before the problem).

 

[anuttarasammyak]

I have not solved it yet but observed that we get another by exchange of variables;
l and x, m and y, n and z in one. And so let
$$xa=X,yb=Y,zc=Z,la=L,mb=M,nc=N$$ the problem is written as
If
$$\frac{X}{L(M+N-L)}=\frac{Y}{M(N+L-M)}=\frac{Z}{N(L+M-N)}=1$$
then prove
$$\frac{L}{X(Y+Z-X)}=\frac{M}{Y(Z+X-Y)}=\frac{N}{Z(X+Y-Z)}$$

We can make the first equation equals to 1 without losing generality. By expressing X,Y,Z by M,N,L using the first equation
$$X+Y-Z=(N+M-L)(N+L-M)$$
$$Y+Z-X=(L+N-M)(L+M-N)$$
$$Z+X-Y=(M+L-N)(M+N-L)$$
and
$$\frac{(Y+Z-X)X}{L}=(N+M-L)(N+L-M)(L+M-N)$$
$$\frac{(Z+X-Y)Y}{M}=(N+M-L)(N+L-M)(L+M-N)$$
$$\frac{(X+Y-Z)Z}{N}=(N+M-L)(N+L-M)(L+M-N)$$
We get the expected result.

 

[brotherbobby]

Your response (@anuttarasammyak) is similar to what I did in post #1, except that I equated all the fractions given to an arbitrary $k$.

I post the solution below as given by the authors. It is incredibly well done and, needless to say, very difficult. I struggled at several places to understand what the authors were doing, let alone try and do it myself !

 

[anuttarasammyak]

It seems to say 1/2 = 2/4 = (1+2)/(2+4). Smart but I think it is mere a technique .