mathmari
Gold Member
MHB
- 4,984
- 7
Hey! 
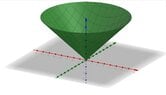
Which region does the set $D=\{(x, y, z) \mid \sqrt{x^2+y^2}\leq z\leq 1\}$ represent?
The surface $z= \sqrt{x^2+y^2}$ is a cone, or not? But why when we want to calculate an integral over $D$ we use cylindrical coordinates? (Wondering)
Which region does the set $D=\{(x, y, z) \mid \sqrt{x^2+y^2}\leq z\leq 1\}$ represent?
The surface $z= \sqrt{x^2+y^2}$ is a cone, or not? But why when we want to calculate an integral over $D$ we use cylindrical coordinates? (Wondering)