- #1
Jhordan
- 5
- 0
Hi, my teacher showed us how we can derive de relation between spectral radiance and density of cavity (of a black hole), but I have a doubt.
This is the equation of the energy that are coming from definited directions by the intervals of angles θ and Φ with frequency in a determined interval:
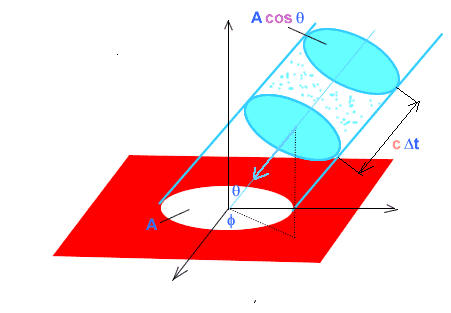
$$
\left[\rho\left(\nu\right)d\nu\right]\cdot\left[\frac{\sin\left(\theta\right)d\theta d\phi}{4\pi}\right]
$$
But if we integrade θ from 0 to π/2 and Φ from 0 to 2π so we has:
$$
\frac{\rho\left(\nu\right)d\nu}{2}
$$
I think that this are because if the body are in thermal equilibriu, same quantity energy that are coming to in are coming out from, so how we onlye need want the nergy that are being irradiated by the black body, we have half of this total of density of energy. I am correct?
Thank you
Link for complete derivation [in portuguese]: https://www.if.ufrgs.br/~betz/iq_XX_A/radTerm/aRadTermAd_1.htm
This is the equation of the energy that are coming from definited directions by the intervals of angles θ and Φ with frequency in a determined interval:
$$
\left[\rho\left(\nu\right)d\nu\right]\cdot\left[\frac{\sin\left(\theta\right)d\theta d\phi}{4\pi}\right]
$$
But if we integrade θ from 0 to π/2 and Φ from 0 to 2π so we has:
$$
\frac{\rho\left(\nu\right)d\nu}{2}
$$
I think that this are because if the body are in thermal equilibriu, same quantity energy that are coming to in are coming out from, so how we onlye need want the nergy that are being irradiated by the black body, we have half of this total of density of energy. I am correct?
Thank you
Link for complete derivation [in portuguese]: https://www.if.ufrgs.br/~betz/iq_XX_A/radTerm/aRadTermAd_1.htm
