- #1
vcsharp2003
- 897
- 177
- Homework Statement
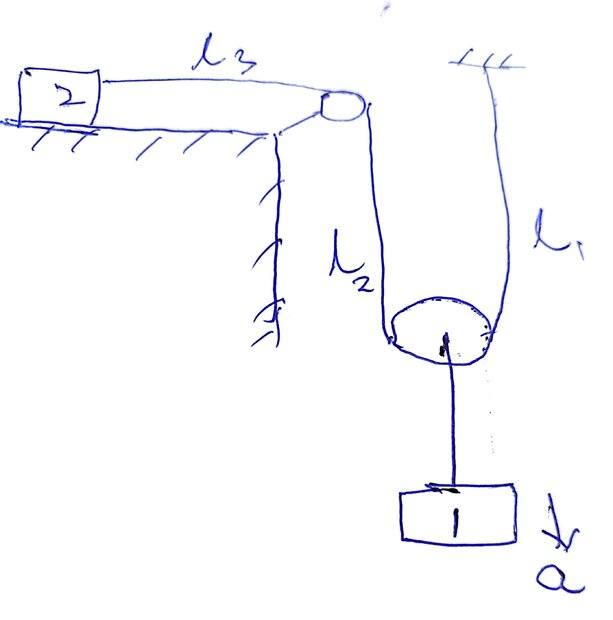
- In the following mass pulley system what would be the relationship between accelerations of blocks 1 and 2? Assume acceleration of block 1 is ##a## downwards, so that ##a## denotes the magnitude of acceleration of block 1.
- Relevant Equations
- None
Assume that the lengths of various sections of the string at an instant are as shown. So we can say that
##l_1 + l_2+l_3= k## at an instant of time ##t##, where ##k## is a constant.
Taking the second derivative of both sides w.r.t. ##t##, we get $$\frac {d^2{l_1}} {dt^2} +\frac {d^2{l_2}} {dt^2} + \frac {d^2{l_3}} {dt^2} = 0$$.
After above step, I'm stuck. I know the second and third terms in LHS will be each equal to ##a##.
$$\therefore \frac {d^2{l_3}} {dt^2} = -2a$$.
I need to now prove that LHS is negative of acceleration of block of 2. How will I prove that?
##l_1 + l_2+l_3= k## at an instant of time ##t##, where ##k## is a constant.
Taking the second derivative of both sides w.r.t. ##t##, we get $$\frac {d^2{l_1}} {dt^2} +\frac {d^2{l_2}} {dt^2} + \frac {d^2{l_3}} {dt^2} = 0$$.
After above step, I'm stuck. I know the second and third terms in LHS will be each equal to ##a##.
$$\therefore \frac {d^2{l_3}} {dt^2} = -2a$$.
I need to now prove that LHS is negative of acceleration of block of 2. How will I prove that?