Relationship between the Different Frequency vs Decibel Graph Peaks

[Darmstadtium]

In the popular answer for the coin-mass question of Physics Stack Exchange,

So, I decided to try it out. I used Audacity to record ~5 seconds of sound that resulted when I dropped a penny, nickel, dime, and quarter onto my table, each 10 times. I then computed the power spectral density of the sound and obtained the following results:

Power spectral density that results from dropping various American coins on a table. I also recorded 5 seconds of me not dropping a coin 10 times to get a background measurement. In the plot, I've plotted all 50 traces on top of one another with each line being semi-transparent.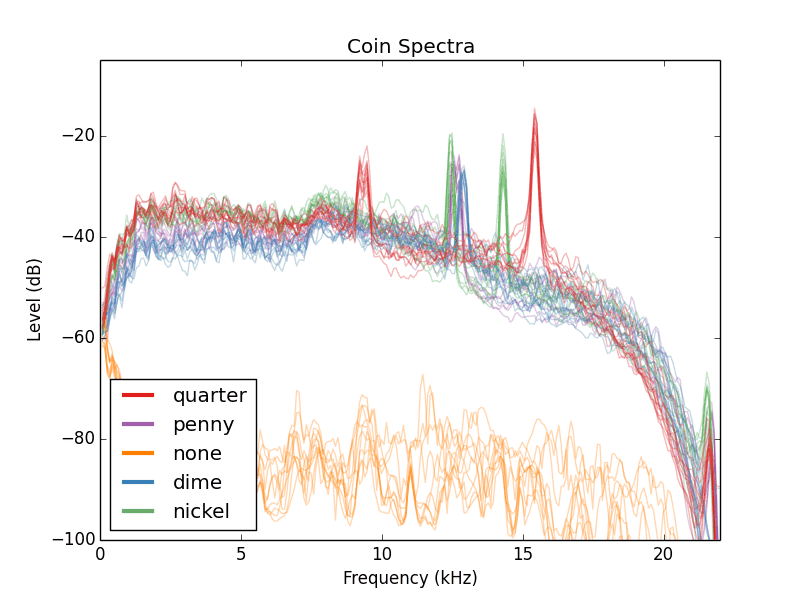

I am wondering what are the correlation between the first red peak at around 9kHz and the second red peak at 16kHz. I first thought that they are consecutive harmonics but there was no way of proving it as I do not know the fundamental harmonic, and they do not differ by 2 nor by 3/2...

And secondly, what causes the peaks at the specific frequencies for the different coins?

Thanks!

 

[Baluncore]

Welcome to PF.

I am wondering what are the correlation between the first red peak at around 9kHz and the second red peak at 16kHz. I first thought that they are consecutive harmonics but there was no way of proving it as I do not know the fundamental harmonic, and they do not differ by 2 nor by 3/2...

Modes of oscillation are not related by integer constants like the harmonics of an oscillation. That is because the dimension of the resonator is measured along a different geometric path for each different mode.

The harmonics of a sinewave, at different integer multiples, arise due to distortion of the fundamental. Since the fundamental waveform pattern repeats, the harmonics must be at integer ratios.

And secondly, what causes the peaks at the specific frequencies for the different coins?

In effect, the dimensions of the coin, and the speed of sound waves in the metal alloy.

For any specific value of coin, the size will remain the same, but the coins may be minted from slightly different alloys over time, so coins may have slightly different masses, speeds of sound, and so slightly different resonant frequencies, depending on the year they were minted.

 

[Darmstadtium]

Thanks for the response, but I don't quite understand the difference between modes of oscillation and harmonics of oscillation. Could you dumb it down a bit for me?

Modes of oscillation are not related by integer constants like the harmonics of an oscillation. That is because the dimension of the resonator is measured along a different geometric path for each different mode.

The harmonics of a sinewave, at different integer multiples, arise due to distortion of the fundamental. Since the fundamental waveform pattern repeats, the harmonics must be at integer ratios.

 

[Baluncore]

Thanks for the response, but I don't quite understand the difference between modes of oscillation and harmonics of oscillation.

There are two quite different effects at play here.

Modes of oscillation.
If you take a straight spring steel bar and twist it slightly, it will spring back and oscillate either side of straight. That is a torsional mode of vibration. If you bend it to a slight 'U' shape, it will spring back to an inverted 'U' and oscillate. Those two modes of oscillation are determined by different geometrical properties, and so cannot be expected to have an integer p/q frequency relationship.
It is only when two modes become physically coupled together that they may lock to the same frequency, but then that will not be a simple torsion mode, or simple bending mode, it will be a more complex, third mode of vibration.

Harmonics of a fundamental.
Take a look at; https://en.wikipedia.org/wiki/Fourier_analysis
Notice that the non-sinusoidal waveform of the bass guitar repeats. The fine detail is held in the amplitude and phase of the harmonics. The shape of the wave would change with time, if the harmonics were not locked to the fundamental.

The distortion of a sinewave will generate odd, and/or even harmonics, depending on the symmetry of the distortion. Bipolar distortion, symmetrical about zero, creates odd harmonics. Unipolar distortion, asymmetric about zero, will create even harmonics. The phase of all harmonics must be related to the fundamental, or it would not repeat.

Harmonics due to distortion are always higher than the fundamental. To generate sub-harmonics, at lower frequencies than the fundamental, at integer multiples of the fundamental time period, some form of energy or information storage must be available. A simple example is an odometer, a digital counter or frequency divider. I would include the iterative Do:Loop or For:Next loop in software, as a generator of sub-harmonics.

A set of harmonics will all have an integer p/q frequency relationship to each other, and to the fundamental.