Relationship of applied load against beam surface strain

[123physics]

Homework Statement

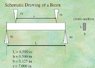
I am working with an electronic bathroom scale and now have to find the relationship of the applied load which is mass in kg against the beam surface strain.
The maximum load is assumed to be 75 kg.

Homework Equations

(M/I)(h/2)=Eε

A picture of the beam has been attached

The Attempt at a Solution

I can calculate the bending moment at one of the ends

ƩM=-R1*L+F1*(L-0,75)+75*0,75 =0
I also know that moment of inertia of a beam is I=bh^3/12
and h is given.

But then I am stuck

Hope some can help be.

Best regards

 

[KataKoniK]

,

As a fellow scientist, I am happy to assist you with this problem. It seems that you have already made some progress in your calculations. The equation you have listed, (M/I)(h/2)=Eε, is known as the flexural strain equation and it relates the bending moment (M) to the applied load (F), moment of inertia (I), height of the beam (h), and the modulus of elasticity (E). This equation can be used to determine the strain in the beam due to the applied load.

To continue with your solution, you will need to determine the reaction force (R1) at the support point and the force (F1) at the other end of the beam. This can be done by taking moments about the support point and using the equation you have already set up. Once you have these values, you can plug them into the flexural strain equation along with the given values for moment of inertia and height to solve for the strain (ε).

It is important to note that the maximum load of 75 kg is assumed, so you will also need to consider the effects of any additional loads that may be applied to the beam. I would recommend setting up a free body diagram of the beam to help visualize the forces acting on it.

I hope this helps guide you towards a solution. Good luck with your calculations!