Marilyn67
- 100
- 20
- TL;DR Summary
- I used two calculation methods and found two completely different results ...
I don't understand !
Hello,
Hope you had a merry Christmas,
In order to deepen some knowledge on the notion of relative simultaneity, I studied a graph taken from a video, and the ages of the twins being very very rounded, I decided to make precise calculations using two methods different.
I would like to point out that this is not a recurring question like those that often come up on this great "classic" of forums.
These two methods both seem consistent to me, yet they don't give me the same result at all.
My question:
Is either of the two methods wrong, and if so, why ?
We know that in relative movement, the situation is symmetrical, that is not the problem, I understood it for a long time.
Here are the starting assumptions, with the attached graph :
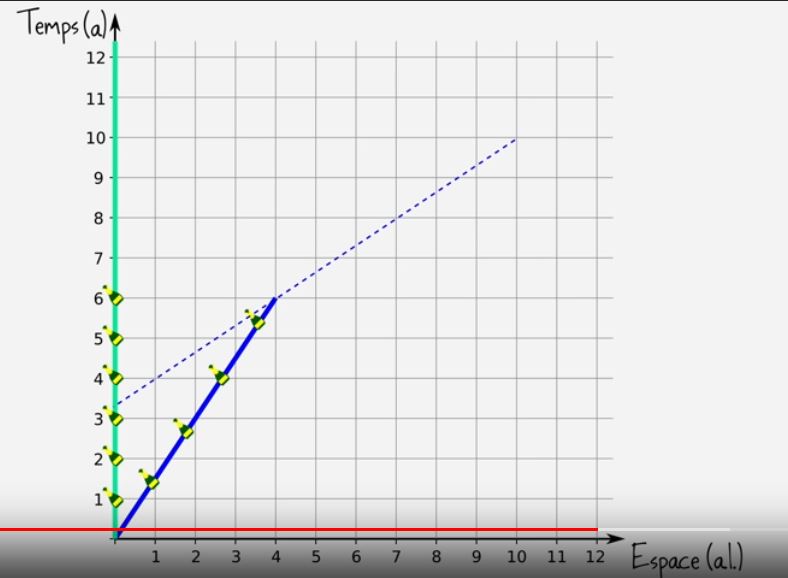
A twin leaves Earth in the direction of Proxima Centauri.
We set the distance D = 4 light years to simplify Its speed represents 2/3 of C. (speed is considered constant over the vast majority of the route, to simplify).
The Lorentz factor is about 1.3416.
Passing next to Proxima Centauri, the spacecraft twin does not stop, it continues its course indefinitely at uniform speed.
For the Earth, it takes 6 years to travel this distance. OK.
For the spacecraft , 4.47 years have passed, and the astronaut is 4.47 years more when passing Proxima Centauri, OK. (6/1.3416)
(Small yellow and green cones represent champagne bottles (birthdays) )
For the astronaut, his simultaneity line (dotted line on the graph) indicates that at this event, his brother on Earth is a little over 3 years more (other event), OK.
How many exactly ?
This is where I used two different calculation methods :
First method :
It consists in saying that for the astronaut aged 4.47 years more, his brother on Earth moves away from him at 2/3 of C, and is therefore affected by the Lorentz factor ɣ = 1.3416.
I find 3.33 years more by simply doing 4.47 / 1.3416.
This result seems fair to me.
Second method :
We have been taught that two simultaneous events in R '( spacecraft frame of reference) moving at a speed v relative to R (earth frame of reference) are separated by a time interval :
Δt '= - ɣ (v / c²). (X'a-X'b)
So I find Δt '= - 1.3416 (2/9). (4 - 0) = -1.1925 years.
In the end, on this line of simultaneity, the terrestrial twin would therefore have 4.47 - 1.19 = 3.28 years more.
You will tell me, the difference is not important ...
So I redid the same calculation with a much larger Lorentz factor (tending to infinity).
What seems incredible to me is that with the first method, the terrestrial twin sees his age approaching 0 years more with the first method, (he has hardly aged), OK, whereas with the second method, Δt 'tends towards -∞, in other words, an arbitrarily distant time in the past, even before the departure of the spaceship, and even before the birth of the terrestrial twin !
It seems crazy to me.
Which result is true, which result is false, and why ?
However, I am sure that the second formula is correct, so I don't understand.
Thank you in advance for your answers !
Cordially,
Marilyn
Hope you had a merry Christmas,
In order to deepen some knowledge on the notion of relative simultaneity, I studied a graph taken from a video, and the ages of the twins being very very rounded, I decided to make precise calculations using two methods different.
I would like to point out that this is not a recurring question like those that often come up on this great "classic" of forums.
These two methods both seem consistent to me, yet they don't give me the same result at all.
My question:
Is either of the two methods wrong, and if so, why ?
We know that in relative movement, the situation is symmetrical, that is not the problem, I understood it for a long time.
Here are the starting assumptions, with the attached graph :
A twin leaves Earth in the direction of Proxima Centauri.
We set the distance D = 4 light years to simplify Its speed represents 2/3 of C. (speed is considered constant over the vast majority of the route, to simplify).
The Lorentz factor is about 1.3416.
Passing next to Proxima Centauri, the spacecraft twin does not stop, it continues its course indefinitely at uniform speed.
For the Earth, it takes 6 years to travel this distance. OK.
For the spacecraft , 4.47 years have passed, and the astronaut is 4.47 years more when passing Proxima Centauri, OK. (6/1.3416)
(Small yellow and green cones represent champagne bottles (birthdays) )
For the astronaut, his simultaneity line (dotted line on the graph) indicates that at this event, his brother on Earth is a little over 3 years more (other event), OK.
How many exactly ?
This is where I used two different calculation methods :
First method :
It consists in saying that for the astronaut aged 4.47 years more, his brother on Earth moves away from him at 2/3 of C, and is therefore affected by the Lorentz factor ɣ = 1.3416.
I find 3.33 years more by simply doing 4.47 / 1.3416.
This result seems fair to me.
Second method :
We have been taught that two simultaneous events in R '( spacecraft frame of reference) moving at a speed v relative to R (earth frame of reference) are separated by a time interval :
Δt '= - ɣ (v / c²). (X'a-X'b)
So I find Δt '= - 1.3416 (2/9). (4 - 0) = -1.1925 years.
In the end, on this line of simultaneity, the terrestrial twin would therefore have 4.47 - 1.19 = 3.28 years more.
You will tell me, the difference is not important ...
So I redid the same calculation with a much larger Lorentz factor (tending to infinity).
What seems incredible to me is that with the first method, the terrestrial twin sees his age approaching 0 years more with the first method, (he has hardly aged), OK, whereas with the second method, Δt 'tends towards -∞, in other words, an arbitrarily distant time in the past, even before the departure of the spaceship, and even before the birth of the terrestrial twin !
It seems crazy to me.

Which result is true, which result is false, and why ?
However, I am sure that the second formula is correct, so I don't understand.
Thank you in advance for your answers !
Cordially,
Marilyn

