Relative Speed of Two Masses Connected by a Rod

[B3NR4Y]

Homework Statement

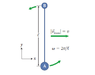
The system shown in consists of two balls A and B connected by a thin rod of negligible mass. Ball A has three times the inertia of ball B and the distance between the two balls is ℓ. The system has a translational velocity of v in the x direction and is spinning counterclockwise at an angular speed of ω=2v/ℓ.
Determine the ratio of the instantaneous speeds of the two balls vA/vB at the moment shown.
The diagram is below.

Homework Equations

I don't know any...

The Attempt at a Solution

Since ball A is traveling in the direction of motion, I added the angular speed and translational speed.
Since ball B is traveling in the opposite direction, I subtracted angular from translational.

$v_{a} = \frac{2v+vℓ}{ℓ}$ and $v_{b} = \frac{vℓ-2v}{ℓ}$ and then when I divided v_A by v _B , I get $\frac{2v+vℓ}{vℓ-2v}$. Not the right answer. The hint I was given by my TA was to get the both in the same units, so I converted angular speed to translational speed and got v as the answer, which is obviously no help because I get 0 in the denominator. Not good...

 

[Simon Bridge]

Relevant equations

I don't know any...

This is not true - you have had 74 (at time or writing) other posts and some of them have relevant equations in them.
You should have some relative velocity equations and notes somewhere.

Determine the ratio of the instantaneous speeds of the two balls vA/vB at the moment shown.

... with respect to what?
This is important because it's a relative velocity problem.

[iline] v_{a} = \frac{2v+vℓ}{ℓ} [/iline] and [iline v_{b} = \frac{vℓ-2v}{ℓ} [/iline] and then when I divided vA by v B , I get [iline] \frac{2v+vℓ}{vℓ-2v} [/iline].

... here, let's see if I can help:
$$v_{a} = \frac{2v+vℓ}{ℓ},\qquad v_{b} = \frac{vℓ-2v}{ℓ},\\
\implies \frac{v_a}{v_b} = \frac{2v+vℓ}{vℓ-2v}$$
... that what you meant?
Doesn't make any sense to me - what was your reasoning behind all that?

The hint from the TA is OK as it goes - but to get the linear velocity from the angular one, you need to know the center of rotation.

 

[B3NR4Y]

And the moment I posted this I figured out the solution. I forgot everything I knew about the problem, and worked from scratch and got an answer of 3. Looking at your post, however, I you would have been massive help. Thank you for your potential help, U(x) ;)

75 posts now.

 

[Simon Bridge]

Working from scratch (just using physics) is the way to go. Well done.