Relative strength of E and B fields in EM radiation

[DiracPool]

I think the equation for the relationship of the E (electrical) and B (magnetic) fields in electromagnetic (EM) radiation is E=Bc, where c is the speed of light.

I think this is correct, but what does it tell us? On it's face, it looks as though the B field (of a photon, say) is 1/300,000,000th the strength of the E field. Is this not correct?

Why, then, do we see these diagrams of the EM propagation of say, light, where the proportion of the E and B field appear to be equal?

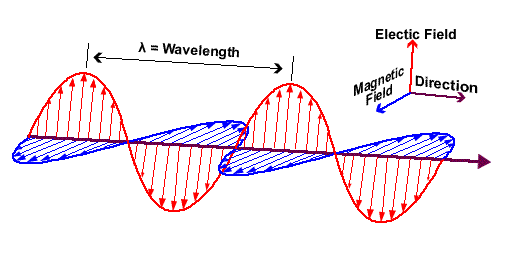
According to that equation, the size of the B field would be almost negligible. So why am I seeing blue lines on this diagram?

I've heard it both ways, though: 1) that the B field is, indeed, much smaller than than the E field in EM radiation, and 2) that they are actually the exact same in field strength. I can spend some valuable time searching for the references but it's going to cost you if you make me do that

I think the counter-argument is that you can just set the speed of light to 1 and then the equation just becomes E=B? Its that simple? And perhaps this is the case because EM radiation is relativistic, and always travels at c so therefore we should set c to one here? Or is this bad logic?

In any case, what is the answer? Are the strengths of the E and B fields identical in a traveling EM wave or is the E field much stronger than the B field?

 

[Khashishi]

No, that's not correct. The magnetic and electric fields of an electromagnetic wave contain equal energy. The numerical value of the electric and magnetic fields depend on the units used, so it doesn't make sense to compare them in the way you are doing. In Gaussian cgs units, the electric and magnetic fields have the same units and can be compared. For a plane wave in vacuum, they are equal.

 

[Dale]

I think this is correct, but what does it tell us? On it's face, it looks as though the B field (of a photon, say) is 1/300,000,000th the strength of the E field. Is this not correct?

This is comparing apples and oranges. Would you say that 1 m was some fraction of 1 kg? If you were plotting m on one axis and kg on another, would you feel compelled to scale them in any particular way?

 

[vanhees71]

Indeed, it's a drawback of the use of SI units in (theoretical) electromagnetics. You can not directly compare the field components althrough they belong together in one field, the electromagnetic field. That's why in theoretical physics one usually prefers Gaussian units (which is a mixture of electrostatic and magnetostatic units) or rationalized Gaussian units (also known as Heaviside-Lorentz units), which are used in high-energy physics and relativistic quantum field theory.

The situation in the SI is somehow a bit like measuring distances in different units, depending on their direction, as in the US, where they measure distances on the road in miles but heights of bridges or mountains in feet.

In the more natural Gaussian-type units the electric and magnetic field components are measured in the same units, and the (non-covariant) Lorentz force on a point charge reads
$$\vec{F}=q \left(\vec{E} + \frac{\vec{v}}{c} \times \vec{B} \right).$$
If you have, e.g., a plane-wave field, you have $\vec{E}^2-\vec{B}^2=0$ in these units, i.e., the magnitude of the electric and the magnetic component of the field is the same, and this is so in any inertial reference frame, because $\vec{E}^2-\vec{B}^2$ turns out to be a Lorentz invariant.

On the other hand, the Lorentz force formula makes it clear, why magnetic forces are often smaller than electric, because you have a factor $\vec{v}/c$ for the magnetic part. For slowly moving charges, thus you have small forces although the magnetic and electric field are of the same magnitude.

The systems of units agree in "mechanical" quantities like energy density as already stated in #2. The energy density of the em. field is
$$\mathcal{E}=\frac{1}{2}(\vec{E}^2 + \vec{B}^2) \quad \text{(Heaviside-Lorentz units)}$$
or
$$\mathcal{E}=\frac{1}{2} \left (\epsilon_0 \vec{E}^2 + \frac{1}{\mu_0} \vec{B}^2 \right) \quad \text{(SI units)}.$$
These conversion factors $\epsilon_0$ and $\mu_0$ make the comparison of the field components difficult. So it's indeed easier to compare the energy densities of the electric and magnetic field to get that kind of intuition about the field components' magnitude.