Relative Velocity of Swimmer: How to Calculate Total Time for Different Paths?

[Taylor_1989]

Homework Statement

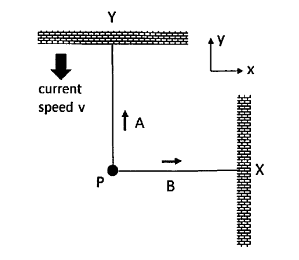
The figure below depicts swimmers A and B who a race. A swim directly from the start point P to point Y (a distance L) and back again. B swims in a direction orthogonal to A from the start point P to point X (also a distance L) and back again. In the absence of any currents, the two swimmers have the same top speed of c. Both swimmer maintain a perfectly straight line through their respective courses and exert a maximum effort throughout.

a) Assume that there is no current. How long dose the journey for each swimmer take?

b) Let us now assume that a current flows with speed v in the negative y direction as shown on the figure. By consideration of the effective component of the velocity vectors along the two directions of travel or otherwise, find an expression for the difference in time of arrival $\Delta t$, of the two swimmers in terms of the time in (a) and the parameter $\beta =v/c$

Relevant Equations

$v=d/t$
$c=\sqrt(a^2+b^2)$

So I was just wondering if someone could check my method for (b) as sometimes I can have a tendency of getting the relative components wrong ect.

Diagram 1

(a)
Time for PY: $T=L/c$
Time for YP: $T=L/c$
Total Time:$2L/c$

(b)
Velocity for PY: $c-v$
Time: $T=L/(c-v)$

Velocity for YP: $c+v$
Time : $T=L/(c+v)$

Total time : $T_{t1}=2cL/(c^2-v^2)$

Now for PX and XP I used the following diagram 2

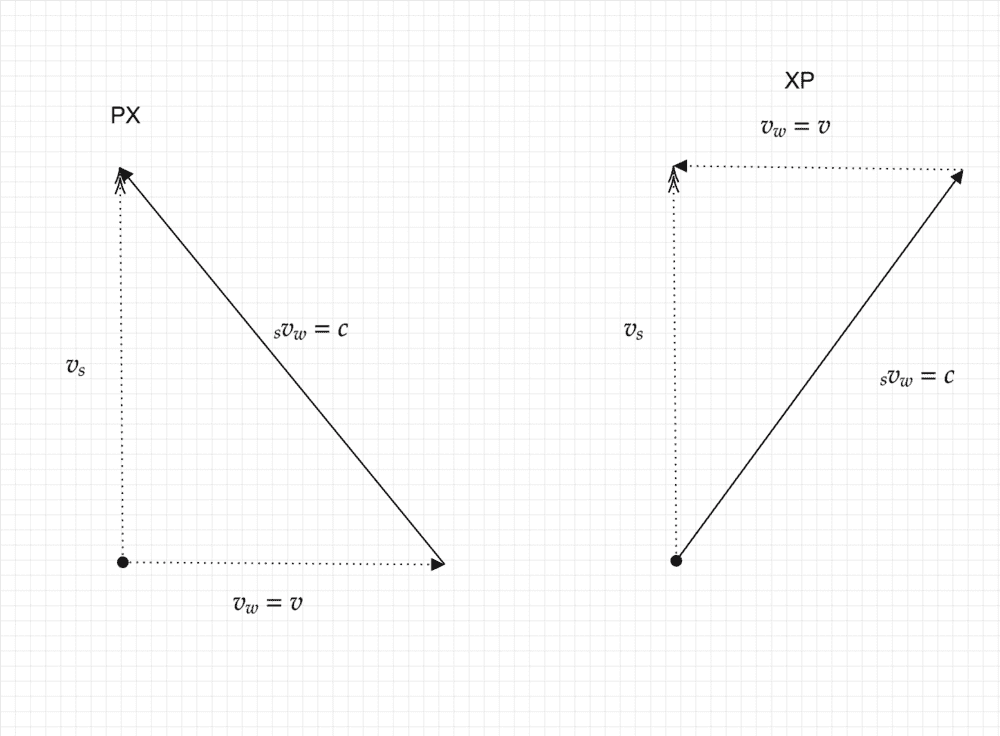
From these I calculated the velocities of PX and XP of the swimmer to be

PX : $v_s=\sqrt{c^2-v^2}$
XP : $v_s=\sqrt{c^2-v^2}$

So calculating the total time

$T_{t2}=\frac{2L}{\sqrt{c^2-v^2}}=\frac{2L\cdot \sqrt{c^2-v^2}}{c^2-v^2}$

Next I simplified $T_{t1}$ and $T_{t2}$

$T_{t1}=\frac{2L}{c\sqrt{1-\beta^2}}$

$T_{t2}=\frac{2L \sqrt{1-\beta^2}}{c(1-\beta^2)}$

so $\Delta T$ is given by

$\Delta T = \frac{2L(\sqrt{1-\beta^2})}{c(1-\beta^2)}$

 

[TSny]

Diagram 2 appears to be rotated by 90 degrees relative to diagram 1. But that doesn't affect your results. Your results for $T_{t1}$ and $T_{t2}$ look correct to me. However, there are some "typos" at the end where you wrote:

Next I simplified $T_{t1}$ and $T_{t2}$

$T_{t1}=\frac{2L}{c\sqrt{1-\beta^2}}$

$T_{t2}=\frac{2L \sqrt{1-\beta^2}}{c(1-\beta^2)}$

so $\Delta T$ is given by

$\Delta T = \frac{2L(\sqrt{1-\beta^2})}{c(1-\beta^2)}$

Did you write $T_{t1}$ correctly here? Note that your expressions for $T_{t1}$ and $T_{t2}$ are equivalent.

What should $\Delta T$ reduce to if $v = 0$? Does your result do this?

You are asked to express $\Delta T$ in terms of the time $T_a$ for part (a).