- #1
Fantini
Gold Member
MHB
- 268
- 0
Hello all. I didn't know whether this fit pre-university math so I posted here. This is exercise's 1.15 from Kleppner & Kolenkow.
By relative velocity we mean velocity with respect to a specified coordinate system. (The term velocity, alone, is understood to be relative to the observer's coordinate system.)
a) A point is observed to have velocity ${\mathbf v}_A$ relative to coordinate system $A$. What is its velocity relative to coordinate system $B$, which is displaced from system $A$ by distance ${\mathbf R}$? (${\mathbf R}$ can change in time.)
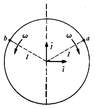
b) Particles $a$ and $b$ move in opposite directions around a circle with angular speed $\omega$, as shown.
View attachment 3286
At $t=0$ they are both at the point ${\mathbf r}=l \vec{j}$, where $l$ is the radius of the circle.
Find the velocity of $a$ relative to $b$.
My thought process for (a): We want to write the velocity of the particle in $B$ given the velocity in $A$. This means we need to write the coordinate system $A$ in terms of the coordinate system $B$, which can be done by noting that ${\mathbf r}_A = {\mathbf r}_B + {\mathbf R}$. Differentiating with respect to time and isolating ${\mathbf v}_B$ we get
$${\mathbf v}_B = {\mathbf v}_A - \frac{d{\mathbf R}}{dt}.$$
This agrees with the book's answer.
My thought process for (b): I wrote
$$\begin{eqnarray} {\mathbf r}_A & =& l \sin(\omega t) \vec{i} + l \cos(\omega t) \vec{j}, \\ {\mathbf r}_B & = & - l \sin (\omega t) \vec{i} + l \cos(\omega t) \vec{j}, \end{eqnarray}$$
for the position vectors, as the picture. This means that
$${\mathbf R} = {\mathbf r}_A - {\mathbf r}_B = 2 l \omega \sin(\omega t) \vec{i}.$$
Using the result from part (a) gives then
$${\mathbf v}_B = {\mathbf v}_A - \frac{d{\mathbf R}}{dt} = - l \omega \cos(\omega t) \vec{i} - l \omega \sin(\omega t) \vec{j}.$$
Is this correct?
By relative velocity we mean velocity with respect to a specified coordinate system. (The term velocity, alone, is understood to be relative to the observer's coordinate system.)
a) A point is observed to have velocity ${\mathbf v}_A$ relative to coordinate system $A$. What is its velocity relative to coordinate system $B$, which is displaced from system $A$ by distance ${\mathbf R}$? (${\mathbf R}$ can change in time.)
b) Particles $a$ and $b$ move in opposite directions around a circle with angular speed $\omega$, as shown.
View attachment 3286
At $t=0$ they are both at the point ${\mathbf r}=l \vec{j}$, where $l$ is the radius of the circle.
Find the velocity of $a$ relative to $b$.
My thought process for (a): We want to write the velocity of the particle in $B$ given the velocity in $A$. This means we need to write the coordinate system $A$ in terms of the coordinate system $B$, which can be done by noting that ${\mathbf r}_A = {\mathbf r}_B + {\mathbf R}$. Differentiating with respect to time and isolating ${\mathbf v}_B$ we get
$${\mathbf v}_B = {\mathbf v}_A - \frac{d{\mathbf R}}{dt}.$$
This agrees with the book's answer.
My thought process for (b): I wrote
$$\begin{eqnarray} {\mathbf r}_A & =& l \sin(\omega t) \vec{i} + l \cos(\omega t) \vec{j}, \\ {\mathbf r}_B & = & - l \sin (\omega t) \vec{i} + l \cos(\omega t) \vec{j}, \end{eqnarray}$$
for the position vectors, as the picture. This means that
$${\mathbf R} = {\mathbf r}_A - {\mathbf r}_B = 2 l \omega \sin(\omega t) \vec{i}.$$
Using the result from part (a) gives then
$${\mathbf v}_B = {\mathbf v}_A - \frac{d{\mathbf R}}{dt} = - l \omega \cos(\omega t) \vec{i} - l \omega \sin(\omega t) \vec{j}.$$
Is this correct?