I Relativity of Simultaneity Questions

[mucker]

Hi All,

I've been doing some reading on the above but having some problems understanding certain parts of it (maybe it's wrong from Wikipedia!) To simplify it for me I will first pose a simple scenario where we are not factoring in speed yet, then go from there.

Say we have two planets A and B and observer A. These planets are exactly 1ly from observer A and explode. Observer A will see and therefore conclude they exploded at the same time. Now let's say observer B is in a position so that he is 1ly away from planet A but 2ly away from planet B. He will observe that plant A exploded first.

My question is, if observer B is a physicist (and therefore is aware that light takes longer to reach him from planet B), and were to document these events, would he record them as how he observed them (not at the same time) or would he record them as happening at the same time (by factoring in the his distance from them)? In other words when we record/talk about simultaneous events (in the scientific sense) do we base it on what we observe, or what we conclude?

More questions to come soon when factoring in speed.

Thanks,

 

[Dale]

having some problems understanding certain parts of it

Yes, the relativity of simultaneity is the single most difficult concept in SR.

In other words when we record/talk about simultaneous events (in the scientific sense) do we base it on what we observe, or what we conclude?

It is about what we conclude. I.e. we are assuming intelligent observers that know the finite speed of light and correct for it.

 

[mucker]

Thanks Dale.

So from the above (when motion is not involved) observer A and observer B would be in agreement that the events happened at the same time. It seems that isn’t the case if motion is involved; take this diagram for example re simultaneity. Here are my questions:

From the blue man’s frame of reference I don’t get how he concludes (assume that’s what the diagram is implying) that the 2 lighting bolts happened at separate times. Is it because he is not aware that he is moving relevant to the lighting bolts? In other words, if he was aware he was moving, he would factor in the speed in and conclude they struck at the same time? Or is due to dime dialation? Or is it something else?

Another thing, I don't see why the above statements in my OP don't seem to be applicable here, it seems we could just use the same reasoning above to a moving object if you know how much you've moved in a set amount of time, would that work?

Just want to say that a fully understand how they observer them different, the bit I am struggling with is how they conclude it differently.

 

[Dale]

(when motion is not involved) observer A and observer B would be in agreement that the events happened at the same time.

Yes. Although B does not receive the light at the same time, B recognizes the finite speed of light, compensates, and concludes that they did happen at the same time.

It seems that isn’t the case if motion is involved;

Yes, even if B is co-located with A at the moment of receiving the light.

Is it because he is not aware that he is moving relevant to the lighting bolts?

The lightning bolts in this diagram are idealized and considered to be instantaneous. They do not have any duration, so they cannot have any speed. They are events, “points” in spacetime.

In other words, if he was aware he was moving, he would factor in the speed in and conclude they struck at the same time?

It is not about awareness. It is about choice. Because the laws of physics are the same in all inertial frames, he is allowed to use the frame where he is at rest if he chooses. Of course, he could also choose to treat himself as moving. Either way, it has nothing to do with unawareness. He is aware of all the motion in the scenario and he is allowed to use the frame where he is at rest.

it seems we could just use the same reasoning above to a moving object if you know how much you've moved in a set amount of time, would that work?

Certainly. If he chooses to treat himself as moving then he will correct for his motion and determine simultaneity according to the frame in which he is moving. But that would make the scenario much less instructive, so here he chooses to analyze things in the frame where he is at rest.

the bit I am struggling with is how they conclude it differently.

You should do the math by hand a couple of times, just to see how it works.

 

[mucker]

thanks Dale.

The lightning bolts in this diagram are idealized and considered to be instantaneous. They do not have any duration, so they cannot have any speed. They are events, “points” in spacetime.

I get that, I was referring to the light rays from the lightning bolts taking time to reach him

It is not about awareness. It is about choice. Because the laws of physics are the same in all inertial frames, he is allowed to use the frame where he is at rest if he chooses. Of course, he could also choose to treat himself as moving. Either way, it has nothing to do with unawareness. He is aware of all the motion in the scenario and he is allowed to use the frame where he is at rest.

I suppose what I am saying is that in the blue man's ref frame it looks like it's only describing what he observed - I mean it doesn't even use words like "conclude" like it does when talking about the green man's ref frame. It looks to me, from the lightning bolts at diff times (very botton frame), that he observed it that way, but says nothing about what he concluded of that observation.

 

[Dale]

I get that, I was referring to the light rays from the lightning bolts taking time to reach him

That is c in all inertial frames.

I suppose what I am saying is that in the blue man's ref frame it looks like it's only describing what he observed - I mean it doesn't even use words like "conclude" like it does when talking about the green man's ref frame. It looks to me, from the lightning bolts at diff times (very botton frame), that he observed it that way, but says nothing about what he concluded of that observation.

That is why I recommend that you go through the math yourself a few times.

 

[mucker]

One last question - does any of this have to do with time dilation at this point? Or can we understand it without having to bring that in?

 

[Ibix]

Time dilation comes in later. At this point we're just proving that "simultaneous" isn't something frames can agree on if the speed of light is invariant. We haven't introduced clocks yet so we can't compare their rates.

It's worth doing the maths to work out when the flashes arrive at the train guy and what ge must conclude about when the flashes happened, as @Dale advised. Post if you get stuck - it's why we're here.

 

[Dale]

One last question - does any of this have to do with time dilation at this point? Or can we understand it without having to bring that in?

All three, time dilation, length contraction, and relativity of simultaneity are important. The Lorentz transform encapsulates all three.

In working out the numbers, you should use the Lorentz transform. And 0.6 c is a good speed to use since relativistic effects are readily visualized and computed but things are still easy to draw.

 

[mucker]

Ok so let's give this a go. I assume you mean the lorentz transformation so I will use the equation from the wikipedia page here.

So before I start I need to know what metric to use. t is obvious but is v and x in metres? Or is v a percent to light speed like Dale used above?

 

[Dale]

is v and x in metres? Or is v a percent to light speed like Dale used above?

You can do it either way, as long as you are consistent. If $v$ is in m/s then $x$ is in m and $t$ is in s and $c$ is in m/s. If $v$ is in light years per year (fraction of $c$) then $x$ is in light years and $t$ is in years and $c=1$. Similarly with light-seconds.

 

[Nugatory]

@mucker Now that @Dale has straightened out the units…. If you’re going to work through an example I suggest that you choose $v=.6c$ or $v=.8c$, measure time in seconds and distances in light-seconds. You will find the arithmetic appreciably less messy.

 

[mucker]

ok I'll do it in m/s.

For the calc below I am using m/s. Ok so let's give this a go. Let t =3 and x=2 and v=1000. Let's just do the top half of t¹ first to make sure my math is correct:
t -vx/c²

= 3-(1000x2)/c2
= 3-(2000/c2)
= 3- 2.225300112107237e-14
=2.999999999999978

Is that right? (just the top half)

for botton half, which is the Lorentz factor I believe?

v2 / c2 = 1,000,000 / 8.987551787368176e+16 = 1.112650056053618e-11
so now we say 1- 1.112650056053618e-11 = 0.9999999999888735
then we square root this = 0.9999999999944367
then it's 1 / 0.9999999999944367
= 1.000000000005563

so t¹ = 2.999999999999978 / 1.000000000005563
= 2.999999999983289

Proably should have used bigger numbers lol. I realize (after doing the calc) I've used low crappy numbers (I was visualising the train example) that it would negilble but can someone just confirm the math is correct?

 

[mucker]

Then to work out x¹ we do top half first:

x-vt
= 2 - 1000*3
= -2998

then bottom half is the Lorentz factor again which we already know from above is 1.000000000005563.

so now 2998 / 1.000000000005563 =
-2997.99999998332000000000

Clearly something is wrong with how I worked out the x¹ location but I can't see where I went wrong?

 

[Nugatory]

but I can't see where I went wrong?

Stop.
Back up and retry your example with a few changes that will make it easier to see what is going on without obscuring the underlying physics:
1) Start with a much larger value of $v$, either .6c or .8c so that the gamma factor comes out to be a reasonable round number, either 5/4 or 5/3
2) Choose units in whic $c$ is equal to one. Seconds and light-seconds will be the closest to something that you can visualize: we all know what a second is, and a light-second is about seven times around the world.
3) Do an Google image search (that's an image search, not a regular one) for "Einstein train simultaneity". Look at some of the graphs that finds.

(Also, be aware that you cannot trust a calculator when working out to 12 or 14 decimal places)

 

[mucker]

Ok so if i change v to 0.6c I get a Lorentz factor of 1.25

So doing it again...
t¹ = top half of equation = t -vx/c2
= 3 - 0.6*2/1²
=3- 1.2
= 1.8

so t¹ = 1.8/1/25 = 1.44 ly
Correct?

NOTE: I had no idea it would get so messy using m/s, which is why I went ahead with it. m/s seemed simpler at the time...

 

[mucker]

Would someone be so kind as to confirm if I have calculated it correctly above?

Also, I've simualated the Einstein thought experiment now in a spreadsheet and it does the Lorentz transformation to show what obervers B should conclude; I'll share a screenshot of it next after I know I've got the formula correct first!

thanks

 

[Ibix]

You've correctly calculated $\gamma=1.25$ but you then seem to have divided by it instead of multiplying.

 

[mucker]

Thanks Ibix.

So the big line separating the top formula from the bottom formula here doesn't mean divide by?

I worked out the top to be 1.8 and bottom as 1.25 (which you said is correct) so from that I see it as top formula outcome divided by bottom formula outcome, therefore 1.8/1.25.

 

[Doc Al]

So the big line separating the top formula from the bottom formula here doesn't mean divide by?

Of course it does, it's a fraction. But the Lorentz factor is one over the bottom formula:
\gamma = \frac{1}{\sqrt{1 - v^2/c^2}}

 

[Ibix]

Thanks Ibix.

So the big line separating the top formula from the bottom formula here doesn't mean divide by?

View attachment 287388
I worked out the top to be 1.8 and bottom as 1.25 (which you said is correct) so from that I see it as top formula outcome divided by bottom formula outcome, therefore 1.8/1.25.

$\sqrt{1-v^2/c^2}=\sqrt{1-0.6^2}=0.8$, but the Lorentz factor is one over that. You can multiply by 5/4 or divide by 4/5.

I can confidently predict that this is not the only time you will make that mistake...

 

[mucker]

Hold on, I think i see your point now Ibex. What you are saying is that I came to the correct answer to work out Lorentz factor but by a different (wrong?) way?

 

[mucker]

Ibix because you didn't mention t and my answer to Lorentz factor was correcton I thought your comment about dividing rather than multiplying was in ref to me calculating t, no?
Thinking about it now, I think you may have misread the post. When I said 1.8/1.25 I was referring to t, I think you thought I was still working out the Lorentz factor at that point?? Just for some context I did use the 1 over formula to work out the Lorentz factor btw - I just didnt show the calculation (well I did in the m/s post), I just shown the outcome (first line). The rest of the post was working out t (which I think you thought was still me working out Lorentz factor??)

 

[Doc Al]

Even though you calculate the Lorentz factor, you need to realize that your equations are not written in terms of that factor. (You are adding it mentally, and making an error.) Try writing your Lorentz transformation equations in terms of $\gamma$, like this:

t' = \gamma( t - v x/c^2)

 

[mucker]

Thanks Doc, I will give that a go. But just to clarify, that equation I quoted is not mine but from Wikpedia. Just want to check - so is the equation (I provided) wrong, or how I interpreted it?

If I use your formula I get 1.25*1.8 = 2.25 correct?

If correct:
Either the original formula I used is wrong or I worked it wrong. If I am wrong, I can't see how:

doesn't equal:
t -vx/c²
/ (divided by)
γ

If I'm wrong, can you please explain where I am getting confused? thanks buddy

 

[Doc Al]

Thanks Doc, I will give that a go. But just to clarify, that equation I quoted is not mine but from Wikpedia. Just want to check - so is the equation (I provided) wrong, or how I interpreted it?

There's nothing wrong with the equations you quoted (interpreted properly). They are just the standard Lorentz transformations. But note that they don't mention or involve the "Lorentz factor" -- you added that bit.

 

[Doc Al]

Thanks Doc, I will give that a go. But just to clarify, that equation I quoted is not mine but from Wikpedia. Just want to check - so is the equation (I provided) wrong, or how I interpreted it?

If I use your formula I get 1.25*1.8 = 2.25 correct?

If correct:
Either the original formula I used is wrong or I worked it wrong. If I am wrong, I can't see how:

View attachment 287397
doesn't equal:
t -vx/c²
/ (divided by)
γ

If I'm wrong, can you please explain where I am getting confused? thanks buddy

In that quoted equation, you are dividing by $\sqrt{1 - v^2/c^2}$, which is NOT $\gamma$. (It's 1/$\gamma$.)

 

[mucker]

But note that they don't mention or involve the "Lorentz factor" -- you added that bit.

I think I see now. These equations are all new to me, I thought
that equation (you just quoted (how do I do that btw?)) was the lorentz factor as it looks so similar to it. I thought there was some kind of typo so I replaced it with the actual Lorentz factor... I am learning...thanks for clearing it up!

 

[mucker]

Ibix thanks Ibex, sorry for being dumb!

 

[Doc Al]

(how do I do that btw?)

I assume you are asking how I wrote the equations that I showed. I used "Latex", a tool for writing math stuff. It's much easier than it looks! You can get started here: https://www.physicsforums.com/help/latexhelp/

 

[Dale]

Ibix thanks Ibex, sorry for being dumb!

As @Ibix said, we have all made that same mistake multiple times on this road.

 

[Ibix]

Ibix thanks Ibex, sorry for being dumb!

It's easy done. I still do it from time to time. To be clear, you correctly calculated $\gamma=1/\sqrt{1-v^2/c^2}$ and correctly calculated $t-vx/c^2$ but then incorrectly combined them as $(t-vx/c^2)/\gamma$ instead of $\gamma(t-vx/c^2)$. As a general policy I'd recommend trying not to mix expressions containing gammas with expressions containing the square root form because if you do it's easy to substitute the wrong value as you did.

 

[mucker]

Yep, so now I've got that out the way and get the math (finally ) let's get back on track to my OP. I am trying to apply it to the train thought experiment. Let's just focus on one lighning bolt for a second.

from observer 1 (green man, stationary) a lighning bolt strikes 2ls away (he knows the distance for this example). He becomes aware of it at t2 obviously. If we were to plot this event on a spacetime diagram from his perspective do we say t=0, x=2ls, or is it actually t=-2, x=2ls? (because the current frame of reference of an observer is always rooted in t=0, so therefore this event lies 2 seconds in his past). I was at first thinking the former but after thinking through it for a while I think you would record it as the latter...

 

[Ibix]

because the current frame of reference of an observer is always rooted in t=0, so therefore this event lies 2 seconds in his past

You're always at t=0? So your watch always reads the same time? That's odd - I might stay in the same place but my watch always advances.

 

[Nugatory]

If we were to plot this event on a spacetime diagram from his perspective do we say t=0, x=2ls, or is it actually t=-2, x=2ls? (because the current frame of reference of an observer is always rooted in t=0, so therefore this event lies 2 seconds in his past). I was at first thinking the former but after thinking through it for a while I think you would record it as the latter...

It is indeed the latter, but not for the reason you say. Negative values of $t$ aren’t necessarily in the past, they’re just before whatever moment we decided to call $t=0$.

 

[Ibix]

It is indeed the latter, but not for the reason you say. Negative values of $t$ aren’t necessarily in the past, they’re just before whatever moment we decided to call $t=0$.

He can record it as either, surely, as long as he records the reception event consistently. The latter might make the maths slightly simpler, but not much. Or am I missing a stated constraint somewhere?

 

[mucker]

You're always at t=0. That's odd - I might stay in the same place but my watch always advances.

What I was getting at is in respect to base observer/inertial frame (as in from what you are going perform your transformations on) - whenever I see spacetime diagrams the worldline of an object always intersects t0 (unless it's been transformed). Another way of looking at it is that say that we plot the wordline of an object at t1x3, t2x4, is that just the same as t0x2, t1x3 if we move the axis's up one second (or wait for one second to pass)? And isn't it essenitally the same thing? What I am saying is that I always see a wordline intercept t=0 so I assumed that is the just the covention we use - as in we can plot a worldline for two events like I just did, and they mean exactly the same thing, but by convention we defer to the t=0 one.

I came to this conclusion based on the assumption that they are the same thing and that all diagrams i see always intercept t=0 at some point, they have to right? cause that is the present moment

EDIT: Maybe another way of me reprasing the question - why would we start drawing a worldline of an object at t1 (in the future) if we can draw it from t0? I can't see a reason to, which is why I proposed that an frame of reference (in the base spacetime diagram) would be rooted in t=0. Am I making sense or not explain myself well?

 

[mucker]

He can record it as either, surely, as long as he records the reception event consistently. The latter might make the maths slightly simpler, but not much. Or am I missing a stated constraint somewhere?

I suppose in a rounabout way, that is what I was asking and actually what I concluded. What I was asking then is if you can plot it both ways, is the norm (convention/standard/whatever) to draw based on the wordline intersecting t0?

EDIT: sorry I misread what you were answering here. Ignore my above comment, willl leave it here so you can see this edit and delete the comment in a bit

 

[Ibix]

You can put your origin anywhere and anywhen you like. However, it's convenient to place it at one event you intend to transform because the Lorentz transform of x=t=0 is really easy. So I would agree that putting the reception event at x=t=0 is sensible, but it's not obligatory.

My point was that you will always pass through t=0 - you cannot avoid it - but you never stay there. Your "because the current frame of reference of an observer is always rooted in t=0" made me think that you thought an observer was stuck at one time in their rest frame, not at one place. Perhaps I misunderstood.

 

[mucker]

https://www.physicsforums.com/members/ibix.365269/ Yeah I was asking about what is more convenient I suppose, or what is the standard way to represent it, as from what I've seen, most spacetime diagrams always show a wordline intercepting t0 and not t1 for example, as it's more intuitive to have it intersect t0

 

[Ibix]

By t0, I take it you mean $t=0$ and not some arbitrary time $t_0$? If so then I agree, but very much caution against saving yourself a keystroke by typing t0 instead of t=0. It'll only confuse people.

 

[mucker]

yep that's what I mean Ibex, I still don't the shorthands yet, thought t0 was just easier to write than t=0, I guess they mean different things...

 

[mucker]

So I have done a spreadsheet which does all the calcs based on some events you type in, but I was getting weird results when I played around with it, but the math was correct. I've realized the problem is that the train thought experiment is very unintuitive which is causing problems in me grasping this, but when I use the "train platform” thought experiment (second one by Daniel Frost) it made sense. The issue that makes the Einstein one difficult to visualise is that the lightning bolts disappear straight away so you can’t plot their location over time (they disappear after a second), so I can only list one event (if working with one bolt).

Anyway, see this snippet of the spreadsheet and I think I now “get it”. So the last question (hopefully hehe) is am I correct in my assessment of the following:

Context first – the spreadsheet for Einstein experiment. Ob1 is stood on the ground as the train goes past. Two bolts go hit exactly the same distance apart, each end of the train (like the thought experiment) and take 5 secs to reach him exactly.

Ob2 is a person moving 0.6 and what he concludes (not observes??) happened - that is, bolt 2 (on the right) happens (t=2.5) before bolt1. Is this assessment correct and do the numbers look good?

 

[mucker]

I can't help but feel there is something wrong with this visualisation of simultaneity. At first I thought they were using Lorentz transformations to work out what happens in mr blue frame. But now I don't think it is. In fact I don't see anything in the diagram that makes anything seem unintuitive - in mr greens frame he sees the bolts as expected (hit at the same time) and concludes the exact (and perfect) sequence of events that mr blue will conclude...without any Lorentz transformation. And all of that actually is easily quite intuitive (I mean it's obvious to conclude that R ray will hit mr blue first), so what's the big deal? i feel like how Mr blue's frame plays out might not be correct (as it's identical to what mr green concludes about blue), I feel like a Lorentz transformation is missing. To put it another way, from the diagram it looks like we don't need to use Lorentz transformations for mr green to conclude mr blues events, which would make the Lorentz transformation obsolete - which I know is definitely not the case. Am I missing something or is it a poor diagram? I feel lke it's howing what he observed, but not what he concluded...

 

[vanhees71]

At least the two Minkowski diagrams at the end look correct to me. I've also some Minkowski diagrams in my SRT manuscript (Sect. 1.2):

https://itp.uni-frankfurt.de/~hees/pf-faq/srt.pdf

 

[Doc Al]

in mr greens frame he sees the bolts as expected (hit at the same time) and concludes the exact (and perfect) sequence of events that mr blue will conclude...without any Lorentz transformation.

The Lorentz transformations are embedded in the fact that each observer sees the same speed of light with respect to themselves. But, as shown in the diagrams, they disagree about whether the lightning flashes were simultaneous. They do agree that Mr. Green receives the light pulses together and Mr. Blue does not, but they draw different conclusions about what that means.

 

[vanhees71]

I find these usual formulations of the 2nd postulate a bit confusing. I think it's better to state that the speed of light for any inertial observer is $c$ independent of the (relative) velocity of the light source. That's also how Einstein stated it in his first paper on relativity (1905).

 

[Dale]

from observer 1 (green man, stationary) a lighning bolt strikes 2ls away (he knows the distance for this example). He becomes aware of it at t2 obviously. If we were to plot this event on a spacetime diagram from his perspective do we say t=0, x=2ls, or is it actually t=-2, x=2ls? (because the current frame of reference of an observer is always rooted in t=0, so therefore this event lies 2 seconds in his past). I was at first thinking the former but after thinking through it for a while I think you would record it as the latter...

You pick whatever origin you like. The origin needn't be at any specific time or place, but once you pick that origin you need to be consistent. So if you choose the origin as the event where the green man receives the light flash then receiving the light flash would be at $(t_r,x_r)=(0,0)$ and emitting the light flash would be at $(t_e,x_e)=(-2,2)$. Of course, if you wanted you could have chosen a different origin, it doesn't matter as long as you are consistent.

I think the usual origin would be chosen such that $(t_r,x_r)=(2,0)$ and $(t_e,x_e)=(0,2)$, but whatever you pick is fine. Just be consistent thereafter.

Is this assessment correct and do the numbers look good?

Yes, I confirm

 

[mucker]

Wow, so much confusion on my part. I was factoring in how long it takes the light to reach the observers which was over complicating it all (and wrong). I didn't realize when doing all the calcs, spacetime diagrams, Lorentz transformations that in fact you are performing them on exactly when they occurred (in your frame of reference). Once you take out the fact you don't need to account for distance traveled etc it becomes a lot less complex and easier to fathom! The word "observer" and "observed" really should be replaced with more intuitive words, as they just lead to confusion lol - I mean when I read statements that start with "x observes y..." I automatically think that those co-ordinates (on paper) need to be transformed (backtracked so to speak) to factor in the speed of light

If anyone is interested about how/where I went wrong, it was when I inputted ob1 x=5, t=5. I used those numbers because I was inputting in how he would observe it, that is if light was emitted 5ls away it would take 5 ls for him to see it. When in fact I should have just used t=0. I see now.

On a side note I would like to share an amazing spacetime tool I found. Has anyone seen this? Not only does it tell you when events occurred in diff ref frames, it also shows when they would be observed too (click the “show light paths” – the visualisation of it is presented very well - so wish I had access to this last week as it would saved me a week’s worth of headaches!

 

[mucker]

So hey guys, I’ve been ill for a week and been meaning to come back to this. There is one more thing that’s been bugging me since raising the OP; I hoped after doing the maths it would be clearer, but it’s not. I still have problems understanding the Einstein thought experiment. Just to be clear, there is another thought experiment by Daniel Frost” which I understood straight away with no difficulty at all – the exact same thought process I applied to the Einstein experiment which confused me, made perfect sense when applied to the Daniel Frost experiment. This (imo) implies to me that there is something missing in Einstein diagram or I should be applying a different thought process to it.

To get to the root of my confusion I’m going to have to go quite deep and explain my thought process step by step so apologies if the post is overly long and confusing, I am trying to give multiple possibilities of how I could interpret the data. To help in visualising my points I have drawn some spacetime diagrams as below.

Let’s start with the Daniel Frost one, as this to me, is more intuitive and I can completely understand the relatively of simultaneity using this example.

In this thought experiment (call it experiment A) an emitter (call it a bulb) emits light at t=0 from the centre of the train (EventA in diagram). From Observer’s A frame of reference (top right diagram) the light takes 5s to hit the front and back of train (Event B and C) at the same time, then a further 5ls to reach him making a total of 10ls. Since he knows the distance of Event B and C he concludes they happen at the same time. This example is very intuitive and easy to understand. Note the two horizonal lines going vertically are the world lines of the train at rest from his perspective (in case that wasn’t clear).

Now look at it from Observer B (left diagram) who is on the platform. From the diagram you can clearly see that the light emitted from EventA reaches the back of the train first, therefore events B and C do not happen simultaneously. All good so far, and I completely understand this too, again very easy to visualise and intuitive. An important fact I’d like to point out here though, is that it is EventA (from Observer B frame) that causes EventB and C to occur at different times, this is important because when we talk about the Einstein experiment next EventA isn’t present. Let’s now apply the same thought process to Einstein’s train experiment.

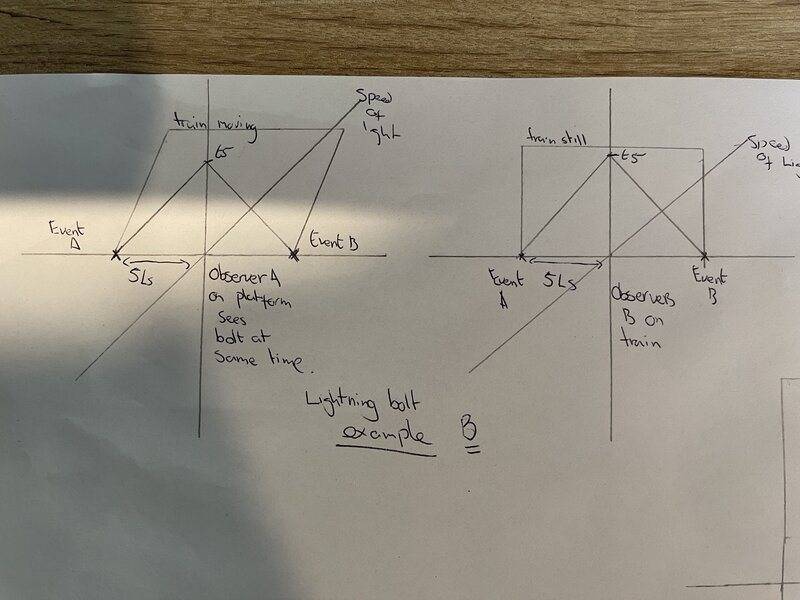
In this example (call it Experiment B) we no longer have an emitter at the centre of the train which strikes the front and back at the same time, instead we just have two lightning bolts hitting at the same time. ObserverA (left diagram) is on the platform and everything plays out as expected and he sees them at the same time. Now, it’s here where things start breaking down for me; I realized that the left diagram in this experiment is really just the same as the left diagram in experiment A…minus the emitter. In other words if we remove EventA (the cause of EventB and C) from experiment A you actually have exactly the same setup as experiment B…yet in experiment B OberserverA sees them at the same time whereas in experiment A the exact same observer doesn’t; so, ALL variables exactly the same in both experiments except the emitter at EventA, and we get different results because of it. Therefore, I came to the conclusion that the cause of Event B and C being out of sync is (at least in part) due to the light from the emitter causing the events to happen out of sync and not necessarily the light emitted from EventsB and C. Can someone please explain what I am missing here and tell how to come up with a thought process which will work for both experiments?

The other issue I can’t get my head around is in relation to the original Einstein diagram with mr green and mr blue. Mr greens concludes that R ray will hit blue before L ray because blue is moving to the right. We know that the speed of light is always the same relative to everyone regardless of your relative speed to something else. So when the two events happen “at the same time” the diagram implies/looks like blue is approaching R ray quicker, but since light never speeds up or slows down relative to you then R ray and L ray (moving at the same speed) should still arrive at the same time, even for him, but they don’t, according to the diagram. I could understand this if we said the speed of light was relative, as this would allow R ray to approach blue quicker, but we know this is not the case. Another way I looked at (which could be wrong, so please tell me if so) is to just forget about Observer A, like imagine he isn’t even there and just focus on Observer B. If the bolts hit at the same time, he will see them at the same time too – exactly like EventB and C in experiment A.

Thanks!