Removable discontinuity solution

[grace77]

Problem statement

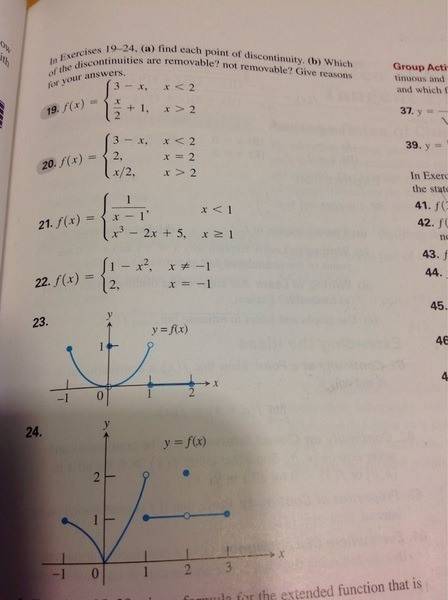Revelant equations

None
Attempt at a solution
I know it is discontinuous if the right hand limit doesn't equals the left hand limit? Is that correct?
The other criteria are
If f(c) exists, lim f(x) x--> c exists and lim f(x)=f(c)

I don't really understand what the other criteria mean? Also how will I tell from the piecewise function if it is removable?

For the graph question number 24 I know the points of discontinuity are the open holes however how do I know if it's removable?

Any help would be appreciated!

 

[jackarms]

Removable means that there's a hole in the graph, as opposed to a break as you would find in a piecewise graph. Removable discontinuities have a hole at a place, and then they're discontinuous immediately to the left and right. They have the missing value (filled in dot) somewhere above or below the hole.

 

[eumyang]

I know it is discontinuous if the right hand limit doesn't equals the left hand limit? Is that correct?
The other criteria are
If f(c) exists, lim f(x) x--> c exists and lim f(x)=f(c)

I don't really understand what the other criteria mean?

For a function to be continuous at a point c, three conditions must be met:
1) f(c) is defined.
The left graph in my attachment shows an example of a graph where f(c) is NOT defined.
2) $lim_{x \rightarrow c} f(x)$ exists.
The middle graph shows an example of a graph where f(c) is defined, but the limit at x = c does not exist.
3) $lim_{x \rightarrow c} f(x) = f(c)$
The right graph shows an example of a graph where f(c) is defined and the limit at x = c exists, but lim f(x) does not equal f(c).

Hope this helps.

 

[grace77]

For a function to be continuous at a point c, three conditions must be met:

1) f(c) is defined.

The left graph in my attachment shows an example of a graph where f(c) is NOT defined.

2) $lim_{x \rightarrow c} f(x)$ exists.

The middle graph shows an example of a graph where f(c) is defined, but the limit at x = c does not exist.

3) $lim_{x \rightarrow c} f(x) = f(c)$

The right graph shows an example of a graph where f(c) is defined and the limit at x = c exists, but lim f(x) does not equal f(c).
Hope this helps.

Oh I understand it now. But how can that be used towards how to do those questions? How would I start?

 

[jackarms]

Here's a good criteria to use:

If $lim_{x \rightarrow c}$ exists and $lim_{x \rightarrow c} \neq f(c)$, then there's a hole at $c$.

If $lim_{x \rightarrow c}$ doesn't exist, but $f(c)$ does exist, then there's a break, as in a piece wise graph that breaks between portions of the domain.

 

[grace77]

Here's a good criteria to use:

If $lim_{x \rightarrow c}$ exists and $lim_{x \rightarrow c} \neq f(c)$, then there's a hole at $c$.

If $lim_{x \rightarrow c}$ doesn't exist, but $f(c)$ does exist, then there's a break, as in a piece wise graph that breaks between portions of the domain.

I understand that thank you but how can I use that to solve the question?

 

[jackarms]

Just apply those formulas to the graphs where there are holes. For example, in 23, there's a discontinuity at x = 0, and in that case the limit exists (f(x) approaches 0 from both sides), but what the graph approaches doesn't equal what the function equals -- i.e. limit approaching c doesn't equal f(c), so then it's a removable discontinuity.

 

[grace77]

Just apply those formulas to the graphs where there are holes. For example, in 23, there's a discontinuity at x = 0, and in that case the limit exists (f(x) approaches 0 from both sides), but what the graph approaches doesn't equal what the function equals -- i.e. limit approaching c doesn't equal f(c), so then it's a removable discontinuity.

Ok thank you how do I do that using a piecewise function without a graph though?

 

[grace77]

Just apply those formulas to the graphs where there are holes. For example, in 23, there's a discontinuity at x = 0, and in that case the limit exists (f(x) approaches 0 from both sides), but what the graph approaches doesn't equal what the function equals -- i.e. limit approaching c doesn't equal f(c), so then it's a removable discontinuity.

Is it that if the 2 sided limits are different then it is not removable?

 

[jackarms]

Yeah, if the left and right limits aren't equal, then it can't be removable.