Renormalization Group:NiemeijerVan Leeuwen Method-Ising Square Lattice

[lapantufla]

Homework Statement

Using the Niemeijer Van Leeuwen method calculate the critical temperature and all
the critical exponents of the Ising model in the square lattice, using the NiemeijerVan Leeuwen approximation to first order in cumulants with a 4-site Kadanoff block. In this case the
majority rule must be generalized to include the case of a tie, in which is assigned
equal probability to both block spin orientations.

Relevant Equations

\sum_{s'}P(s',s)=1

Hello, I have to solve this problem. I will apply the Niemeijer Van Leeuwen method once I have the probability distribution
proper to the renormalization group ,P(s,s'). For example, in the case of a triangular lattice, this distribution is:

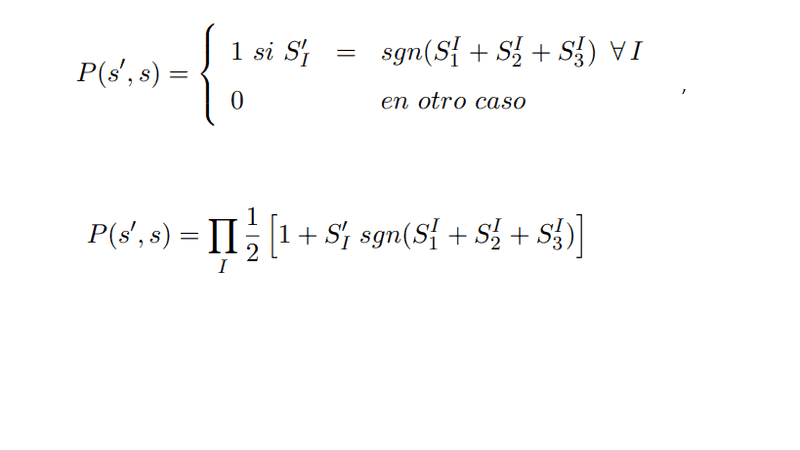
where I is the block index. However, it is very difficult for me to generalize the majority rule for a Kadannof block with even sites, like square lattice. It occurred to me generalize like this:

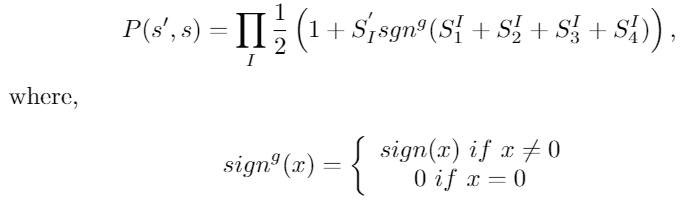
but this distribution is not normalized, that is, it does not satisfy:

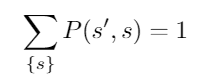
Is anyone able to construct this probability distribution?
Thank you very much.

 

[Nate810]

Yes, it is possible to construct the probability distribution for a Kadannof block with even sites such as a square lattice. The general form of the probability distribution can be written as:P(s,s')=\frac{1}{I}\sum_{i=1}^{I}\delta_{s_i,s'_i}where I is the number of blocks and $\delta_{s_i,s'_i}$ is the Kronecker delta function which is equal to 1 if $s_i = s'_i$ and 0 otherwise. To normalize this probability distribution, you need to make sure that\sum_{s,s'}P(s,s')=1This can be done by multiplying $P(s,s')$ by a factor of $I$. Thus, the normalized probability distribution for a Kadannof block with even sites such as a square lattice is given by:P(s,s')=I\sum_{i=1}^{I}\delta_{s_i,s'_i}