- #1
ai93
- 54
- 0
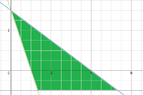
\(\displaystyle 3x+4y\le12\)
\(\displaystyle 3x+y\ge3\)
\(\displaystyle y\ge-1\)
I understand the how to plot these on a graph, just not sure how to solve these inequalities!
Do you have to solve for x or y?
\(\displaystyle 3x+y\ge3\)
\(\displaystyle y\ge-1\)
I understand the how to plot these on a graph, just not sure how to solve these inequalities!
Do you have to solve for x or y?