Trysse
- 75
- 16
- TL;DR Summary
- Reprise to an old thread to which I found a solution (kind of)
https://www.physicsforums.com/threads/b-calculate-the-distance-between-two-points-without-using-a-coordinate-system.1014046/#post-6622205
About two years ago I had a thread here, where I was looking for a way to calculate the distance between two points A and B on a plane when the following information is given:
https://www.physicsforums.com/threa...ing-a-coordinate-system.1014046/#post-6622205
Despite some helpful input, the thread did not get me the answer I was hoping for. So I let the problem rest for a while. Only recently have I come back to this problem. Again I did not find a universal solution for any arbitrary set of reference points. However, this time I have found that I can calculate the distance AB if the three reference points have a specific configuration:
If three reference points O, X and Y form a right-angled triangle, I can calculate the distance between the two points A and B from the distances AO, AX, AY, BO, BX and BY. The right angle XOY can be realized using Pythagorean triples so I don't need to think about constructing right angles.
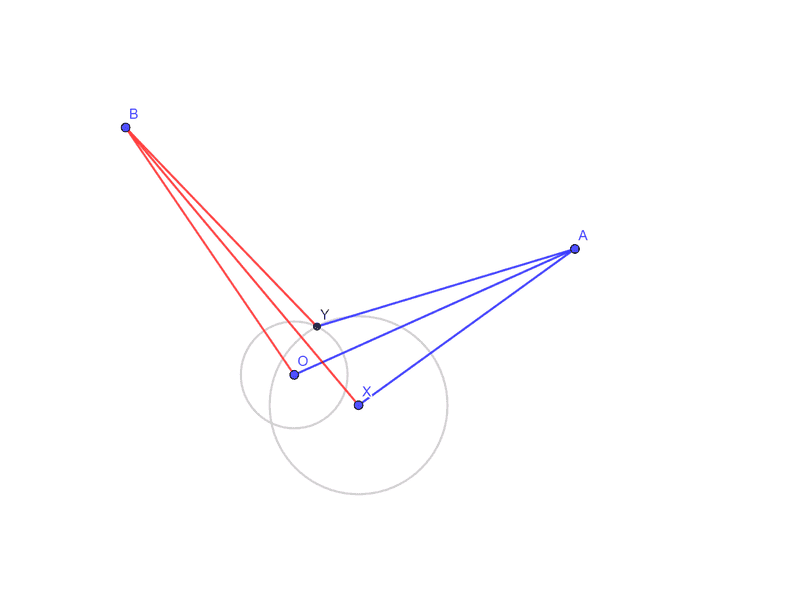
For the calculation of distance and coordinates on a plane and in space see the following Geogebra models. The calculated distance is called AtoB in both files:
What I find nice about this approach, is that I can also calculate cartesian coordinates for points without the need for infinite axes and with only distances (i.e. no angles or directions or perpendiculars and no need to calculate roots (at least for the coordinates)). It has given me a new perspective on cartesian coordinates and the relation between coordinates and invariant distances. I thought this is quite neat!
The related principle is trilateration https://en.wikipedia.org/wiki/Trilateration
From what I have found online this seems to be of more interest for engineering than for geometry/math. https://www.sciencedirect.com/topics/engineering/trilateration
So, although I am no longer looking for a general solution, if you have one, let me know.
- The distances of the points A and B to three arbitrary (but non-colinear) reference points.
- The distances between the three reference points.
https://www.physicsforums.com/threa...ing-a-coordinate-system.1014046/#post-6622205
Despite some helpful input, the thread did not get me the answer I was hoping for. So I let the problem rest for a while. Only recently have I come back to this problem. Again I did not find a universal solution for any arbitrary set of reference points. However, this time I have found that I can calculate the distance AB if the three reference points have a specific configuration:
If three reference points O, X and Y form a right-angled triangle, I can calculate the distance between the two points A and B from the distances AO, AX, AY, BO, BX and BY. The right angle XOY can be realized using Pythagorean triples so I don't need to think about constructing right angles.
For the calculation of distance and coordinates on a plane and in space see the following Geogebra models. The calculated distance is called AtoB in both files:
What I find nice about this approach, is that I can also calculate cartesian coordinates for points without the need for infinite axes and with only distances (i.e. no angles or directions or perpendiculars and no need to calculate roots (at least for the coordinates)). It has given me a new perspective on cartesian coordinates and the relation between coordinates and invariant distances. I thought this is quite neat!
The related principle is trilateration https://en.wikipedia.org/wiki/Trilateration
From what I have found online this seems to be of more interest for engineering than for geometry/math. https://www.sciencedirect.com/topics/engineering/trilateration
So, although I am no longer looking for a general solution, if you have one, let me know.