Freixas
- 307
- 42
- TL;DR Summary
- I’m planning to write a 2D Minkowsky spacetime diagram generator tool. At this point, I am looking for help reviewing the specification.
I’m planning to write a 2D Minkowsky spacetime diagram generator tool. At this point, I am looking for help reviewing the specification. I am not looking for help with the implemenation.
To be clear, I’ve written a complete specification, but it would be a waste if it was missing features that could make it useful to others. I’m willing to share the tool for free if there’s interest.
History
Some years ago, I wrote the first generation of a Minkowski spacetime diagram generator. Version 1 is still running and I used it to create the diagrams at the end of this post. Version 2 had a lot more features and was working, but I trashed it on the way to version 3.
The second generation tool, the one for which I’ve written a specification, is what I imagined version 3 would be. The reason v3 never came to be is because it really needed to be a full rewrite, and not an upgrade from v2. But v1 and v2 provided the practical experience that has shaped my thinking for generation 2.
I posted about v1 on this forum to a deafening silence. It may be that the people here have little need or interest in 2D Minkowski spacetime diagrams. It might be of more interest to physics teachers, for example, because I see it as a teaching and learning tool. I don’t know how to reach that audience—tips are welcome.
Feedback
There are specific types of feedback that I would appreciate:
Diagrams are drawn using a custom script language (there is no way a user interface could provide enough options to handle generic problems—most user-interface-driven tools I’ve seen model variations of a single problem).
The current specification allows the script to:
I’m not going to waste more space here. I’ve place a PDF of the specification at:
It includes a one-page overview and a one-page syntax. The syntax is explained in detail starting at page 5. A section on the user interface follows, and then a set of examples. The sixth sample has nine variations and illustrates how one can start with a specific problem and then vary either the problem, the visualization, or both.
Sample Diagram with Variations
Here is the sample problem:
Keep in mind that the various scripts that follow have not been tested since the tool doesn’t yet exist. The diagrams were drawn with my gen 1 version 1 tool and may also have errors. Since I can’t do animation, I capture one moment in time and then use arrows to indicate what’s moving. The final variation is too tough for me to even try to draw.
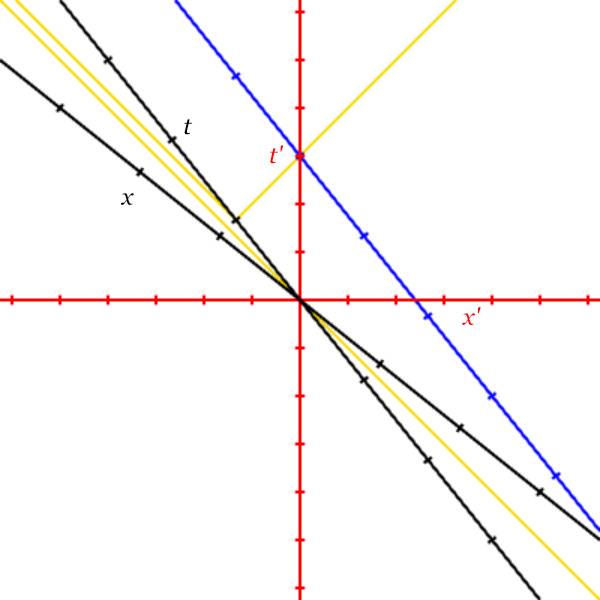
Variation 2
animation reps: 1;
# Add these lines before the axes commands
Variation 3
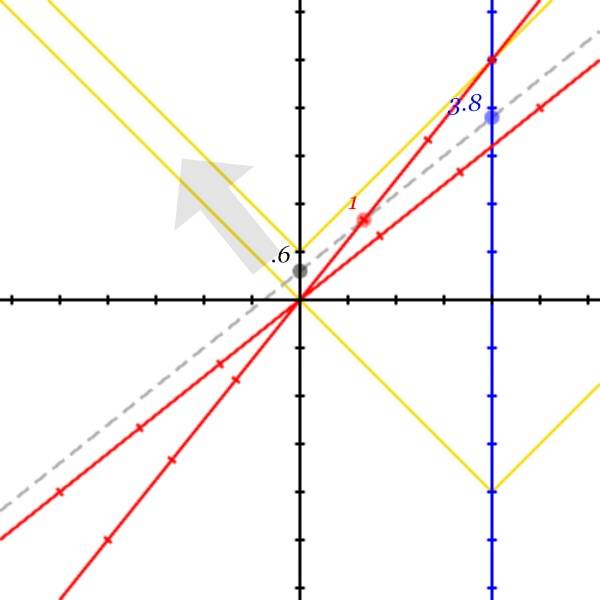
Variation 4
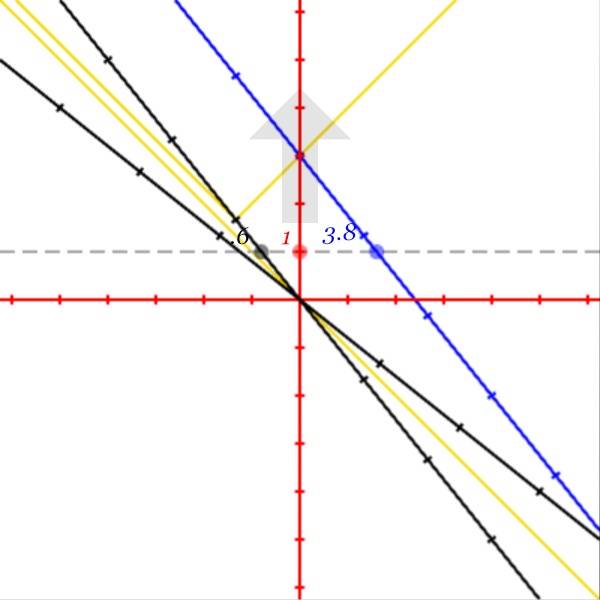
Variation 5
Variation 6
Variation 7

Variation 8
Variation 9
To be clear, I’ve written a complete specification, but it would be a waste if it was missing features that could make it useful to others. I’m willing to share the tool for free if there’s interest.
History
Some years ago, I wrote the first generation of a Minkowski spacetime diagram generator. Version 1 is still running and I used it to create the diagrams at the end of this post. Version 2 had a lot more features and was working, but I trashed it on the way to version 3.
The second generation tool, the one for which I’ve written a specification, is what I imagined version 3 would be. The reason v3 never came to be is because it really needed to be a full rewrite, and not an upgrade from v2. But v1 and v2 provided the practical experience that has shaped my thinking for generation 2.
I posted about v1 on this forum to a deafening silence. It may be that the people here have little need or interest in 2D Minkowski spacetime diagrams. It might be of more interest to physics teachers, for example, because I see it as a teaching and learning tool. I don’t know how to reach that audience—tips are welcome.
Feedback
There are specific types of feedback that I would appreciate:
- Sources for Minkowsky spacetime diagrams (I’ve used Google image search, so it would have to be something more interesting).
- Particular problems that you’d like to diagram.
- Features you’d like to have in a Minkowsky spacetime diagram generator.
- Offers to review the tool’s specification to look for missing features or missed opportunities.
- This tool is for standard2D Minkowsky spacetime diagrams. If there are useful variants, you could make a case for them.
- This tool is for 2D diagrams, not for 3D diagrams (or projections of 3D diagrams onto 2D). When I search for spacetime diagrams, I do get a number of images showing cones representing past and future light cones. All these diagrams look pretty much the same and seem to be illustrating the same thing.
- Quite a few diagrams show hyperbolic curves. As I understand them, a single curve shows all the various coordinates for a specific point in spacetime as seen from every possible inertial frame. I might include these if someone could point out the value of having such a curve in illustrating a particular problem (as opposed to illustrating a general principle) and could also suggest how such a curve might be specified.
- The diagrams are for problems in special relativity. I’m not sure how general relativity problems could be included, but am open to suggestions.
Diagrams are drawn using a custom script language (there is no way a user interface could provide enough options to handle generic problems—most user-interface-driven tools I’ve seen model variations of a single problem).
The current specification allows the script to:
- Draw axes for any inertial frame with proper angles and units
- Automatically label axes and tick marks
- Include unlimited observers
- Create worldline to consist of segments of constant velocity or constant acceleration
- Draw lines and fills
- Draw events
- Draw arbitrary labels
- Draw the lines, fills, and text using various styles (colors, dashed lines, arrowheads, fonts, etc.)
- Save diagrams as image files
- Set up a diagram relative to a rest frame; draw it relative to any inertial frame
- Perform some math operations and special functions provided with the ability to store results in variables
- Create flexible animations
- Pan and zoom the diagram
I’m not going to waste more space here. I’ve place a PDF of the specification at:
It includes a one-page overview and a one-page syntax. The syntax is explained in detail starting at page 5. A section on the user interface follows, and then a set of examples. The sixth sample has nine variations and illustrates how one can start with a specific problem and then vary either the problem, the visualization, or both.
Sample Diagram with Variations
Here is the sample problem:
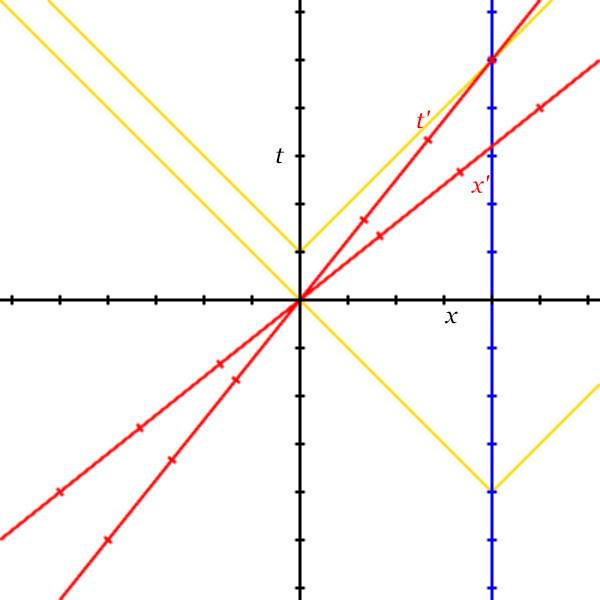
Let Bob and Ted be two observers four light years apart and at rest. Let Alice be an observer on a path from Bob to Ted at a constant velocity of 0.8 c. When Alice reaches Bob, Bob’s and Ted’s clocks read 0 (relative to either Bob or Ted). Alice’s clock also reads 0 (relative to Bob and Alice). Ted sends a light signal to Bob at Ted’s clock time of -4 years. Bob sends a light signal to Ted at Bob’s clock time of 1 years.
Keep in mind that the various scripts that follow have not been tested since the tool doesn’t yet exist. The diagrams were drawn with my gen 1 version 1 tool and may also have errors. Since I can’t do animation, I capture one moment in time and then use arrows to indicate what’s moving. The final variation is too tough for me to even try to draw.
let bobColor = [style color: black];
let tedColor = [style color: blue];
let aliceColor = [style color: red];
let lightColor = [style color: yellow];
let textStyle = [style font: “Georgia”, slant: italic];
let bobStyle = [style bobColor, textStyle];
let tedStyle = [style tedColor, textStyle];
let aliceStyle = [style aliceColor, textStyle];
let bob = [observer ];
let ted = [observer origin (4, 0)];
let alice = [observer velocity 0.8];
let tedColor = [style color: blue];
let aliceColor = [style color: red];
let lightColor = [style color: yellow];
let textStyle = [style font: “Georgia”, slant: italic];
let bobStyle = [style bobColor, textStyle];
let tedStyle = [style tedColor, textStyle];
let aliceStyle = [style aliceColor, textStyle];
let bob = [observer ];
let ted = [observer origin (4, 0)];
let alice = [observer velocity 0.8];
let signal1 = [line angle -45 point (4, -4)];
let signal2 = [line angle +45 point (0, 1)];
let signal2 = [line angle +45 point (0, 1)];
axes frame: ted, x: false, tedStyle;
axes frame: bob, xLabel: “x”, tLabel “t”, bobStyle;
axes frame: alice, xLabel: “x’”, tLabel “t’”, aliceStyle;
line line: signal1, clip: (4, -4) (inf, inf);
line line: signal2, clip: (0, 1) (inf, inf);
Variation 1
Start with the original script, but draw the diagram with Alice as the rest observer.
# Add this line anywhere
diagram frame: alice;
axes frame: bob, xLabel: “x”, tLabel “t”, bobStyle;
axes frame: alice, xLabel: “x’”, tLabel “t’”, aliceStyle;
line line: signal1, clip: (4, -4) (inf, inf);
line line: signal2, clip: (0, 1) (inf, inf);
Variation 1
Start with the original script, but draw the diagram with Alice as the rest observer.
# Add this line anywhere
diagram frame: alice;
Variation 2
Start with the original script and animate the positions of the three observers along bob’s line of simultaneity. Display each observer’s clock where the simultaneity line intersects the observer.
# Add these lines at the top
let animation t = 0 to 5 step .01;
# Add these lines at the top
let animation t = 0 to 5 step .01;
animation reps: 1;
# Add these lines before the axes commands
let simul = [line axis x bob offset t];
let bobLoc = intersect(simul, bob);
let tedLoc = intersect(simul, ted);
let aliceLoc = intersect(simul, alice);
# Add these lines at the end
event location: bobLoc, label: tauFromT(t, bob), bobStyle;
event location: tedLoc, label: tauFromT(t, ted), tedStyle;
event location: aliceLoc, label: tauFromT(t, alice), aliceStyle;
let bobLoc = intersect(simul, bob);
let tedLoc = intersect(simul, ted);
let aliceLoc = intersect(simul, alice);
# Add these lines at the end
event location: bobLoc, label: tauFromT(t, bob), bobStyle;
event location: tedLoc, label: tauFromT(t, ted), tedStyle;
event location: aliceLoc, label: tauFromT(t, alice), aliceStyle;
line line: simul, color: #AAA, dashed: true;
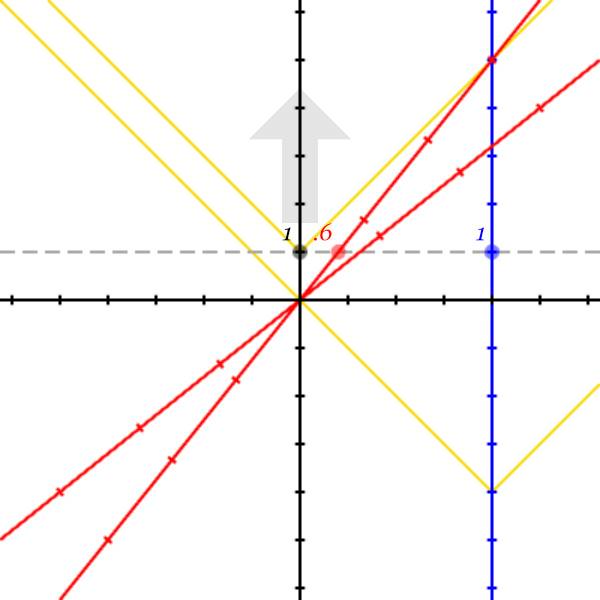
Variation 3
Start with variation 2 but now using Alice’s line of simultaneity. The diagram is still from Bob’s viewpoint.
# Change the animation assignment to
# Change the animation assignment to
let animation t = 0 to 3 step .01;
# Change the simul variable to
let simul = [line axis x alice offset t];
# Change the simul variable to
let simul = [line axis x alice offset t];
Variation 4
Start with variation 3 but now draw the diagram from Alice’s viewpoint.
# Add this line anywhere
diagram frame: alice;
# Add this line anywhere
diagram frame: alice;
Variation 5
Start with variation 2. We will just show the events and use the animation’s time represent the time axis—each frame of the animation will be one-dimensional view. We will see Alice’s dot move from a steady dot representing Bob to a steady dot representing Ted. Each observer’s clock time is displayed by each dot.
# Add this line anywhere after t is defined.
diagram frame: [observer origin (0, -t)];
# Add this line anywhere after t is defined.
diagram frame: [observer origin (0, -t)];
# Remove the axes and line statements
Variation 6
Start with variation 2. Again, we will just show the events and use the animation’s time to represent the time axis, but from Alice’s viewpoint this time. We will see Bob’s dot move away from Alice’s dot (which won’t move). We will also see Ted’s dot move toward and reach Alice’s dot. Each observer’s clock time is displayed by each dot.
# Change the animation assignment to
# Change the animation assignment to
let animation t = 0 to 3 step .01;
# Change the simul variable to
# Change the simul variable to
let simul = [line axis x alice offset t];
# Add these lines anywhere
let alicePos = (0, t < alice);
diagram frame: [observer origin alicePos, velocity 0.8];
# Remove the axes and line statements
diagram frame: [observer origin alicePos, velocity 0.8];
# Remove the axes and line statements
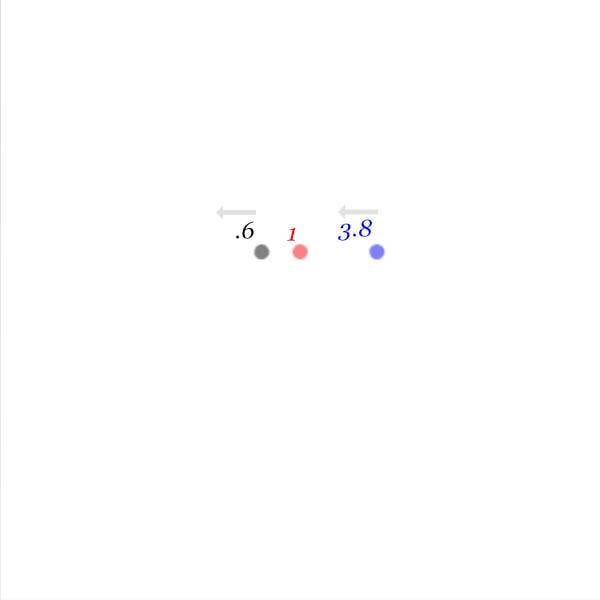
Variation 7
Start with variation 1, but let’s display Bob and Ted in the positions that Alice would see them. Also , display the clock times Alice would see. Note that I had to zoom out to get Ted's event dot in the attached diagram, so the scale is different from all the other diagrams.
# Remove everything after the “let alice = ...” statement
# Remove everything after the “let alice = ...” statement
# Add these lines
let animation t = 0 to 3 step .01;
let aliceLoc = (0, t, <alice);
let lightLine = [line angle +45 point aliceLoc];
let bobLoc = intersect(lightLine, bob);
let lightLine = [line angle -45 point aliceLoc];
let tedLoc = intersect(lightLine, ted);
event location: aliceLoc, label: t, aliceStyle;
event location: (tedLoc.x, t), label: tedLoc.t, tedStyle;
event location: (bobLoc.x, t), label: bobLoc.t, bobStyle;
let lightLine = [line angle +45 point aliceLoc];
let bobLoc = intersect(lightLine, bob);
let lightLine = [line angle -45 point aliceLoc];
let tedLoc = intersect(lightLine, ted);
event location: aliceLoc, label: t, aliceStyle;
event location: (tedLoc.x, t), label: tedLoc.t, tedStyle;
event location: (bobLoc.x, t), label: bobLoc.t, bobStyle;
diagram frame: [observer origin alicePos, velocity 0.8];
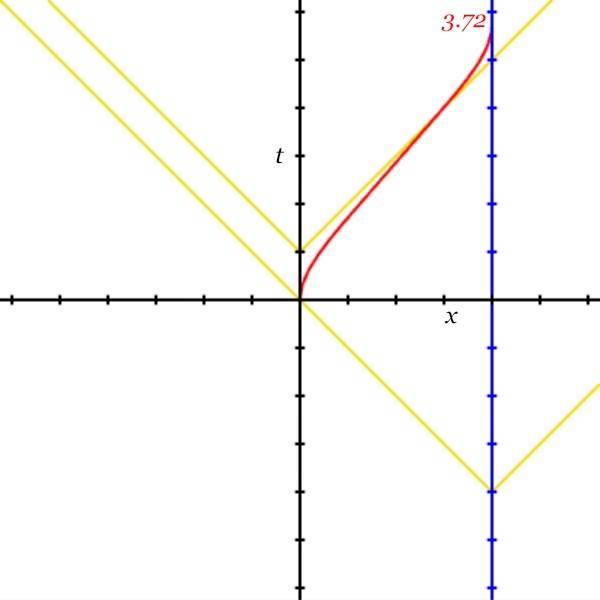
Variation 8
Start with the original script.
Alice now starts he journey in the same rest frame as Bob and Ted. She accelerates at 1g until she is one light year from Bob (as measured by Bob). She coasts until she is one light year from Ted (as measured by Bob). She then decelerates at 1g until she reaches Ted, where her acceleration ends. She should now be in Bob’s and Ted’s rest frames again.
Display Alice’s ending clock time at her ending position.
# Replace the assignment to Alice’s observer variable to this
let alice = [observer acceleration 1 d 1, velocity d 3, acceleration 1 d 1];
Alice now starts he journey in the same rest frame as Bob and Ted. She accelerates at 1g until she is one light year from Bob (as measured by Bob). She coasts until she is one light year from Ted (as measured by Bob). She then decelerates at 1g until she reaches Ted, where her acceleration ends. She should now be in Bob’s and Ted’s rest frames again.
Display Alice’s ending clock time at her ending position.
# Replace the assignment to Alice’s observer variable to this
let alice = [observer acceleration 1 d 1, velocity d 3, acceleration 1 d 1];
# Remove Alice’s axes
# Add this at the end
let aliceTau = tauFromD(5, &alice);
worldline observer: alice, clip: (0, 0), (4, inf), aliceStyle;
label location: (4, aliceTau), text: aliceTau;
# Add this at the end
let aliceTau = tauFromD(5, &alice);
worldline observer: alice, clip: (0, 0), (4, inf), aliceStyle;
label location: (4, aliceTau), text: aliceTau;
Variation 9
Start with variation 8, but animate the display so we can use Alice as the rest observer. Since Alice is accelerating, her rest frame is not consistent. Each frame of the animation will use her instantaneous moving frame at her point in time. I didn't try to create the diagram.
# Add these lines somewhere after &alice is defined
# Add these lines somewhere after &alice is defined
let animation tau = 0 to tauFromT(5, &alice) step .01;
animation reps: 1;
animation reps: 1;
# Add this line anywhere after &alice and tau are defined
diagram frame: [frame alice at tau tau];