Required tension of rope around a cylinder to hold a object.

[kaar]

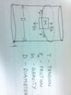
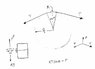
please see attached drawing. I am trying to understand how this would work.

Imagine a vertical cylinder of diameter "D". I would like to tie a mass M to it, using a rope. what is the tension "T" that is required on the rope?

I assume the force required will depend on the coefficient of friction between the cylinder and the mass, let us assume that to be "mu".

but in this case, friction force = mu * force perpendicular to the cylinder surface

how to calculate this perpendicular force? is it just equal to the tension T? I am confused because when a rope goes though a pully we always assume tension to be tangential to the pully at any given point...

any clarifications of my understanding is welcome!

 

[Spinnor]

I have redrawn the problem a bit, I think the physics remains the same. Hope this helps.

 

[Spinnor]

You wrote,

is it just equal to the tension T?

No in general. I think you would have to accurate dimensions of the mass M to calculate what fraction of T presses mass M against the cylinder. My sketch above takes liberty with the dimensions as none were given.

 

[kaar]

That clarified my doubt..thanks.