Resistive circuit - ladder problem

[Rectifier]

Hey!
1. The problem
Figure shows a very long ladder where every part has a resistanse of R. What is the resistance between A and B if the ladder can be approximated to be semi-infinite (the ladder has a beginning but no end).2.The figure

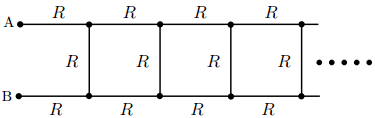3. The attempt
The first three resistances have a resistance of 3R the next step add 3R in parallel to R. The next step after that provides 3 more resistances in parallel with on of the resistances in step two.

Step 1: $3R$ [$2R+\frac {3R}{3}$]
Step 2: $\frac{3R \cdot R}{R+3R}+2R=2R+\frac{3R}{4}$
Step 3: $2R+\frac{3R}{5}$
Step 4: $2R+\frac{3R}{6}$
Step 5: $2R+\frac{3R}{7}$

There is a pattern here. Namely
$Rab=2R+\frac {3R}{2+n}$ for n> 0 and n being integer.

The answere is 2.73 but i get 2.000... something for high values on n.

Please help me.

 

[phinds]

You might want to recalculate step 3

 

[NascentOxygen]

There was one of these questions just recently. The technique for solving it involves drawing a vertical line and saying the resistance to the right of that line equals the resistance seen from terminals A and B. Let's call it M. You can redraw the circuit so it looks much simpler now, and solve for M.

 

[Rectifier]

You might want to recalculate step 3

Is this right for step 3?
$\frac{41R}{15}$

 

[Rectifier]

There was one of these questions just recently. The technique for solving it involves drawing a vertical line and saying the resistance to the right of that line equals the resistance seen from terminals A and B. Let's call it M. You can redraw the circuit so it looks much simpler now, and solve for M.

I am not that I have heared of this technique before. I will try to use it anyway. At what "step" should I draw the line?

Btw, is there a name for it so I can read more about it?

 

[NascentOxygen]

I am not that I have heared of this technique before. I will try to use it anyway. At what "step" should I draw the line?

Draw it where the network remaining to its right will look exactly like the network you started with.

Btw, is there a name for it so I can read more about it?

I can't think of a good name for it right now.

 

[ehild]

We think the way that the resultant resistance X does not change if one unit of the ladder is added or removed from the infinite number of units. See picture of the ladder and the equivalent circuit. Solve for x.

ehild

 

[Rectifier]

Draw it where the network remaining to its right will look exactly like the network you started with. I can't think of a good name for it right now.

Thank you for the reply.

Okay. Let's say I draw a vertical line at step 2 "above" the resistor that is connected in parallell with the rest of the crcuit. Now I am left with 2 identical circuits.

How do I continue now?

 

[BvU]

The technique is called: realizing you have the same situation if you cut off the leftmost three resistors. So apparently the whole thing has the same resistance as 2R + R//(the whole thing).

// meaning: parallel to in my sloppy notation

(If you are as lazy as I am, you want to draw the line at the first step where it makes sense, but not so far as to cause more work than absolutely necessary).

I don't have a good word for the approach: assume you know the answer and work backwards isn't good enough. Someone else ?

 

[Rectifier]

Thank you for your replies I will read and comment back in some minutes.

EDIT:
I will have a lecture now and I will ask the professor if he has time. Sorry that I am being dumb on this one.

 

[NascentOxygen]

Thank you for the reply.

Okay. Let's say I draw a vertical line at step 2 "above" the resistor that is connected in parallell with the rest of the crcuit. Now I am left with 2 identical circuits.

How do I continue now?

Let's say the total resistance of the circuit on the right is equivalent to a resistance M.

You can also say that when you add 3 resistors to that resistor M you make a circuit which again has an equivalent resistance M.

Solve for M.

Perhaps this approach could be called a recursive technique!

 

[BvU]

Re technique: at some point I learned to deal with geometric series, e.g.$$S =1+{1\over2}+{1\over 4} + {1\over 8} + \dots$$and the way to tackle them is to distinguish that $${1\over 2}S = {1\over2}+{1\over 4} + {1\over 8} + \dots$$so that $$S = 1+ {S\over 2}$$see the analogy ?

 

[phinds]

Is this right for step 3?
$\frac{41R}{15}$

No, it's not what I get. How about you show your work (in detail, step by step, and DRAW the exact circuit you are analyzing in that step)

 

[ehild]

Is this right for step 3?
$\frac{41R}{15}$

Yes, it is right.
What is the next?

Evaluating the results, you have a sequence 3R, 2.75R, 2.733R ... They appear to tend somewhere. The differences get smaller and smaller. At the end, the difference between the last two elements of the sequence is so small that they can be considered the same.
If you have the nth term, the n+1th is R_n+1=2R+RR_n/(R+R_n), and at the end you can consider R_n+1=R_n. What do you get for R_n?

ehild

 

[phinds]

Yes, it is right.

Damn. I guess *I* must have made a mistake. Perhaps you can show me where I went wrong.

OOPS. NEVER MIND. I just didn't expand it the way you did. We agree.

https://www.physicsforums.com/newreply.php?do=newreply&p=4839495

 

[ehild]

OOPS. NEVER MIND. I just didn't expand it the way you did. We agree.

I am glad to hear.

ehild

 

[Rectifier]

Let's say the total resistance of the circuit on the right is equivalent to a resistance M.

You can also say that when you add 3 resistors to that resistor M you make a circuit which again has an equivalent resistance M.

This is what my professor told me too. But I don't understand why you get the same resistance when you add stuff :,(.

 

[Rectifier]

the resultant resistance X does not change if one unit of the ladder is added or removed
ehild

Thanks for the comment.

Why not?

 

[Rectifier]

The technique is called: realizing you have the same situation if you cut off the leftmost three resistors. So apparently the whole thing has the same resistance as 2R + R//(the whole thing).

Here it is again
Cant get it to add up like that in my head.

 

[Rectifier]

I read the thread more careful and found the answer to my question above in a thread above.

"At the end, the difference between the last two elements of the sequence is so small that they can be considered the same."

$R_{ab}=R+R//R_{ab}+R \\ R_{ab}=2R+\frac{R \cdot R_{ab}}{R+R_{ab}} \\ R_{ab}(R+R_{ab})=2R(R+R_{ab})+R \cdot R_{ab} \\ R_{ab} \cdot R+R_{ab}^2=2R^2+2R_{ab}\cdot R+R \cdot R_{ab} \\ R_{ab}^2=2R^2+2R_{ab}\cdot R \\ 2R^2+2R_{ab}\cdot R-R_{ab}^2=0 \\$

Solve for $R_{ab}$ where $R_{ab}>0$

$R_{ab}^2-2 R \cdot R_{ab}-2R^2=0 \\ R_{ab}= R \pm \sqrt{R^2+2R^2} \\ R_{ab}= R \pm R\sqrt{3}$

$R_{ab}= (1 + \sqrt{3})R$ since $R_{ab}= (1 - \sqrt{3})R$ is undefiened.

Yey! :D It is the right answer.

 

[ehild]

Only the + sign gives valid solution. R_ab can not be negative. But you have solved it! Congratulation!

The sequence of resistances, as you calculated them, converges very fast to (1+√3)R = 2.7320R. The fourth is 2.7321R already.

ehild

 

[Rectifier]

Re technique: at some point I learned to deal with geometric series, e.g.$$S =1+{1\over2}+{1\over 4} + {1\over 8} + \dots$$and the way to tackle them is to distinguish that $${1\over 2}S = {1\over2}+{1\over 4} + {1\over 8} + \dots$$so that $$S = 1+ {S\over 2}$$see the analogy ?

No, sorry. I am not so farsighted :,(. I guess it something similar with my series of resistances. I am afraid I am not that good at series.

$$S = 1+ {S\over 2}$$ is true indeed. I couldn't have seen that from the equation.

 

[Rectifier]

Thank you to all of you who took their time and helped me. I really appreciate that.

 

[NascentOxygen]

This is what my professor told me too. But I don't understand why you get the same resistance when you add stuff :,(.

Well, if you added some resistance in series with the input you would increase the resistance, and if you added some resistance in parallel you would decrease the resistance, so if you add some of both---correctly chosen---you can reproduce the same resistance!