Resistors in parallel with a capacitor, total resistance?

[Tangeton]

Hello, I am not quite sure how to work out the before and after charging values for resistance and current.
This is the circuit I am working with:

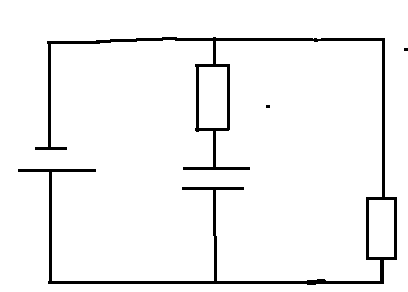
So, when there is no voltage then the capacitor can be technically not considered as part of the circuit. So for the resistors, would R = 1/R1 (the one most to the left) + 1/R2 (the one to the right). but here is my problem.

In this video () at 1:10 ish she faces a similar circuit, and if I was to get rid of that once resistor in series for her the resistance would be (1/R + 1/R)^-1. But why would she inverse 1/R + 1/R and in my case would this apply as well?

 

[FactChecker]

The resistance of the circuit changes as the capacitors charge up. When there is no charge on the capacitors, they act just like a wire connection, so the capacitor on the left shorts out the resisters and the circuit resistance is 0. When the capacitors are fully charged, they act like a broken wire and the circuit acts like the resister on the right.

 

[Tangeton]

The resistance of the circuit changes as the capacitors charge up. When there is no charge on the capacitors, they act just like a wire connection, so the capacitor on the left shorts out the resisters and the circuit resistance is 0. When the capacitors are fully charged, they act like a broken wire and the circuit acts like the resister on the right.

Thanks for your help! But by the resistor on the left... there's only one capacitor so no need to specify I guess..? The element on the left is battery.

 

[STEMucator]

Resistances in parallel obey this rule (which can be verified):

$$R_{||} = \left( \sum_{i=1}^{n} \frac{1}{R_i} \right)^{-1} = \left(\frac{1}{R_1} + \frac{1}{R_2} + \cdots + \frac{1}{R_n} \right)^{-1}$$

Initially assuming the capacitor is uncharged, it behaves like a short circuit. So the equivalent resistance in the circuit is the two resistors in parallel.

After finding the equivalent resistance, you can simply use Ohm's law to find the initial current.

After a long time, the capacitor is fully charged, and stops current from flowing in the branch.

At this time, you have a single loop circuit with an emf. Use KVL or Ohm's law directly to calculate the current.

 

[CWatters]

Equivalent circuit before and after charging the capacitor..

 

[FactChecker]

The element on the left is battery.

Oh! Sorry. Of course. (I shouldn't try to do anything in the morning before a cup of coffee)

 

[gneill]

The resistance of the circuit changes as the capacitors charge up. When there is no charge on the capacitors, they act just like a wire connection, so the capacitor on the left shorts out the resisters and the circuit resistance is 0. When the capacitors are fully charged, they act like a broken wire and the circuit acts like the resister on the right.

That's not quite right, (ideal) capacitors never exhibit resistance. As they charge up they look like a voltage source, V = Q/C, where Q is the charge on the capacitor. When a capacitor is uncharged V = 0 so it looks like a 0 V voltage source (a short circuit, equivalent to a piece of wire). When the circuit reaches steady state and the capacitor is as charged as it's going to get it looks like a voltage source that matches the potential difference between the nodes to which it's connected; current ceases flowing to or from the capacitor since there's no potential difference to drive it, so the capacitor is then effectively an open circuit as it no longer affects the circuit behavior.

 

[Tangeton]

Thanks for everybody's help I understand it now, gneli's post and CWatters's diagrams is what I've been looking for :)