Goliatbagge
- 10
- 1
Suppose we have a vertical circular motion with gravity according to the image below.
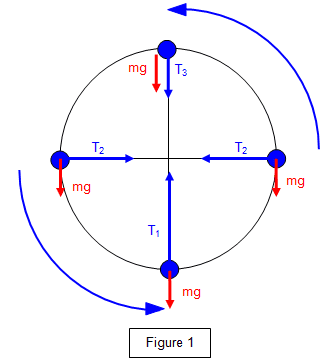
In the leftmost and rightmost positions the resultant force is pointing diagonally down. Isn't the resultant force supposed to be pointing at the center at all times in a circular motion? What am I getting wrong?
In the leftmost and rightmost positions the resultant force is pointing diagonally down. Isn't the resultant force supposed to be pointing at the center at all times in a circular motion? What am I getting wrong?