Resulting force forward from a flat sail

[cosy]

I wanted to calculate the best angle for a sail on a reach, but realized I had to make the calculation a bit unrealistic by using a flat sail and doing other simplifications to make it possible for me to solve. However it seems that wasn't enough ([emoji4]) since I ended up with a quite useless answer, so I was hoping that I could get some help on here! Here is my approach (not that I assumed all sideways force was counteracted by a centerboard):
I started by assuming we had a sail that was 1m*1m and the pressure from the wind was 1N/m^2 (I just needed a constant). I then defined the area catching wind as cos(x)* the area of the sail, so the area will be cos(x)m^2.

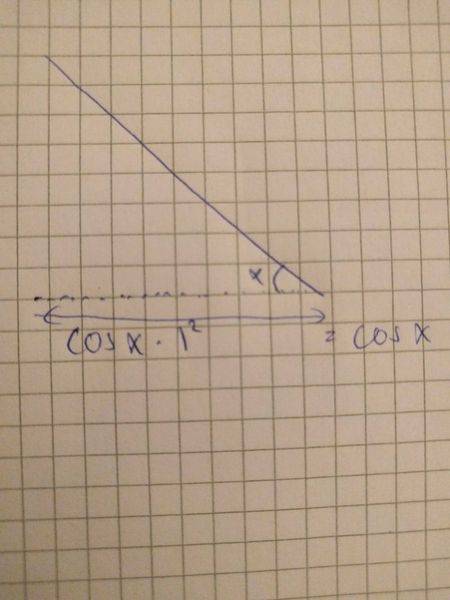
That also means that the total force on the sail will be cos(x)N.
This vector can be divided into the drag (which I will ignore for this calculation) and the lift which will be cos(x)^2.

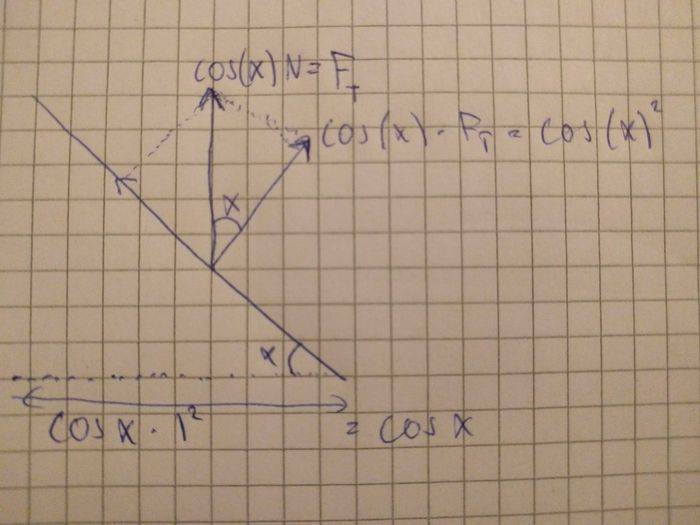
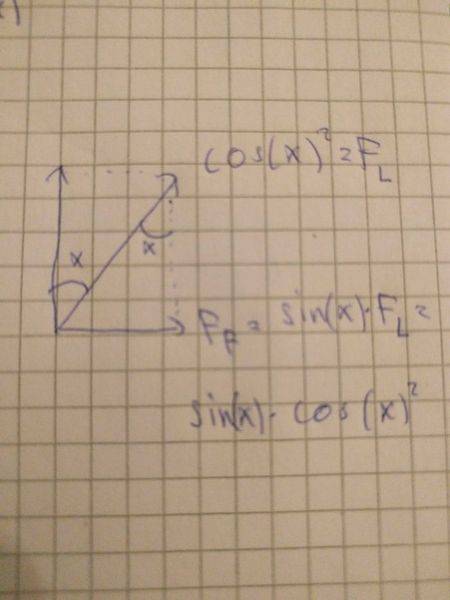
The lift itself can be divided into sideways force and force forward. The force forward will be sin(x)*cos(x)^2.

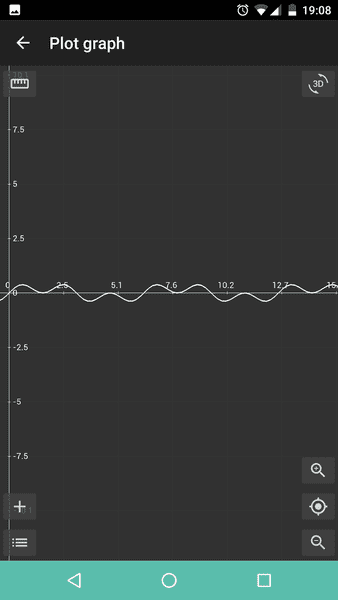
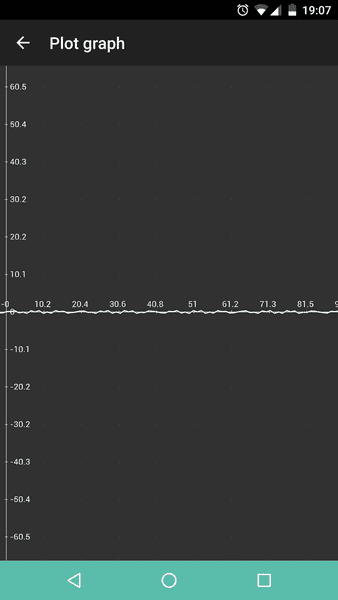
This result however does not make for a satisfying answer as the graph for the function is repetitive and looks like this:

I was expecting to get a curve looking something like this:

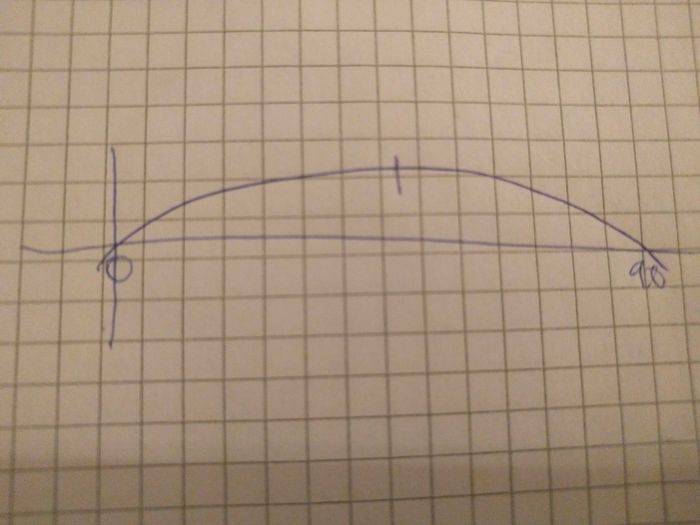
where I could find the point where the derivative was 0 to get the maximum value.
So my question is, of course: What did I do wrong? Thanks for any help in advance!

 

[cosy]

I forgot to point out that something was wrong about my funtion on a very deep level since the value of the function at x=90 was >0!

 

[JBA]

It has taken me a bit of of mental thrashing to work this out but the fact is that since the direction of travel is always perpendicular to the direction of the wind then the amount of force available to move the boat forward: F push = F wind x (sail area x Cos Θ) x Sin Θ = F wind x sail area x Tan Θ.
That formula will give you: Tan Θ = 0 at Θ = 0° and Θ = 90°; and, Tan Θ = 1 at Θ = 45°

At Θ = 0°, F sail = 100% (the face of the sail is perpendicular to the wind) but the perpendicular F push vector = 0% of that force and at Θ = 90° the F sail = 0% (the face of the sail is parallel to the wind), while the F push = 100% of that force.